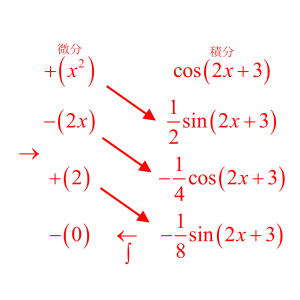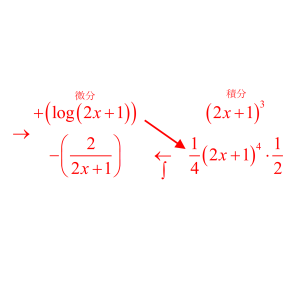第2次導関数
1.次の関数の第2次導関数を求めよ。
(1) $y=(3x-5)^4$
解答
公式 $\{(ax+b)^n\}^{\prime}=an(ax+b)^{n-1}$ を用いる
$y^{\prime}=3\cdot4(3x-5)^3=12(3x-5)^3$
$y^{\prime\prime}=12\{3\cdot3(3x-5)^2\}=108(3x-5)^2$ (答)
(2) $y=e^{5x^2-2}$
解答
公式 $\left(e^{f}\right)^{\prime}=f^{\prime}e^{f}$、$(f\cdot g)’=f’g+fg’$ を用いる
$y^{\prime}=10xe^{5x^2-2}$
$y^{\prime\prime}=10e^{5x^2-2}+10x\left(10xe^{5x^2-2}\right)=10(10x^2+1)e^{5x^2-2}$ (答)
(3) $y=\mathrm{log}(x+1)$
解答
公式 $(\mathrm{log}f)^{\prime}=\dfrac{f’}{f}$、$\left(\dfrac{1}{g} \right)^{\prime}=\dfrac{-g’}{g^2}$ を用いる
$y^{\prime}=\dfrac{1}{x+1}$
$y^{\prime\prime}=\dfrac{-1}{(x+1)^2}$ (答)
(4) $y=\mathrm{sin}3x$
解答
公式 $(\mathrm{sin}(ax+b))^{\prime}=a\mathrm{cos}(ax+b)\;\left((\mathrm{cos}(ax+b))^{\prime}=-a\mathrm{sin}(ax+b)\right)$ を用いる
$y^{\prime}=3\mathrm{cos}3x$
$y^{\prime\prime}=-9\mathrm{sin}3x$ (答)
2次近似
2.次の関数の( )内の値における2次近似を求めよ。
(1) $f(x)=x^5+1\;(x=1)$
解答
$x=a$ での2次近似の公式 $f(x)\fallingdotseq f(a)+f'(a)(x-a)+\dfrac{1}{2}f^{\prime\prime}(a)(x-a)^2$ を用いる
$f(x)=x^5+1,f'(x)=5x^4,\;f^{\prime\prime}(x)=20x^3\;\to\;f(1)=2,f'(1)=5,f^{\prime\prime}(1)=20$
$f(x)\fallingdotseq f(1)+f'(1)(x-1)+\dfrac{1}{2}f^{\prime\prime}(1)(x-1)^2$
$f(x)\fallingdotseq 2+5(x-1)+10(x-1)^2$ (答)
(2) $f(x)=e^{2x}\;(x=0)$
解答
$x=a$ での2次近似の公式 $f(x)\fallingdotseq f(a)+f'(a)(x-a)+\dfrac{1}{2}f^{\prime\prime}(a)(x-a)^2$ を用いる
$f(x)=e^{2x},f'(x)=2e^{2x},\;f^{\prime\prime}(x)=4e^{2x}\;\to\;f(0)=1,f'(0)=2,f^{\prime\prime}(0)=4$
$f(x)\fallingdotseq f(0)+f'(0)(x-0)+\dfrac{1}{2}f^{\prime\prime}(0)(x-0)^2$
$f(x)\fallingdotseq 1+2x+2x^2$ (答)
(3) $f(x)=\mathrm{log}(x+1)\;(x=0)$
解答
$x=a$ での2次近似の公式 $f(x)\fallingdotseq f(a)+f'(a)(x-a)+\dfrac{1}{2}f^{\prime\prime}(a)(x-a)^2$ を用いる
$f(x)=\mathrm{log}(x+1),f'(x)=\dfrac{1}{x+1},\;f^{\prime\prime}(x)=\dfrac{-1}{(x+1)^2}$
$\to\;f(0)=\mathrm{log}1=0,f'(0)=1,f^{\prime\prime}(0)=-1$
$f(x)\fallingdotseq f(0)+f'(0)(x-0)+\dfrac{1}{2}f^{\prime\prime}(0)(x-0)^2$
$f(x)\fallingdotseq x-\dfrac{1}{2}x^2$ (答)
関数のグラフ(増減と凹凸)
3.次の関数の増減・極値・凹凸・変曲点を調べてグラフを書け。
(1) $y=x^3-3x^2$
解答
方針:方程式 $y’=0$ および $y^{\prime\prime}=0$ を解いて、増減表をかく
$y’=3x^2-6x=3x(x-2)=0\;\to \begin{cases}x=0,\hspace{7pt} 2\\y=0,-4\end{cases}$
$y^{\prime\prime}=6x-6=6(x-1)=0\;\to \begin{cases}x=\hspace{7pt}1\\y=-2\end{cases}$
これより増減表を作成してグラフを書くと
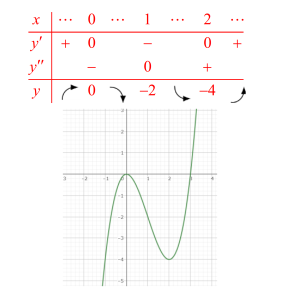
極大値 $0\;(x=0)$、極小値 $-4\;(x=2)$、変曲点 $(1,-2)$ (答) (2) $y=\dfrac{1}{4}x^4-\dfrac{3}{2}x^2$
解答
方針:方程式 $y’=0$ および $y^{\prime\prime}=0$ を解いて、増減表をかく
$y’=x^3-3x=x(x^2-3)=0\;\to \begin{cases}x=-\sqrt{3},0, \sqrt{3} \\y=\dfrac{-9}{4}, \hspace{6pt} 0, \dfrac{-9}{4} \end{cases}$
$y^{\prime\prime}=3x^2-3=3(x^2-1)=0\;\to \begin{cases}x=-1,\hspace{6pt} 1\\y=\dfrac{-5}{4},\dfrac{-5}{4}\end{cases}$
これより増減表を作成してグラフを書くと
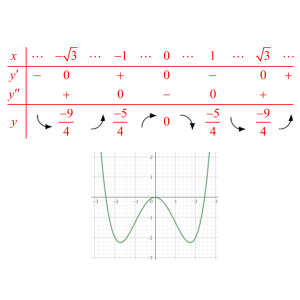
極大値 $0\;(x=0)$、極小値 $\dfrac{-9}{4}\;(x=\pm\sqrt{3})$、変曲点 $\left(\pm 1,\dfrac{-5}{4}\right)$ (答)
いろいろな関数のグラフ
1.次の関数の増減・極値・凹凸・変曲点を調べてグラフを書け。
(1) $y=x\mathrm{log}x\;(x>0)$
解答
3Q_4H3参照(3Q_4H3の演習と同じ問題です)
(2) $y=\dfrac{1}{x^2-1}$
解答
3Q_4H4参照(3Q_4H4の演習と同じ問題です)
(3) $y=x\sqrt{4-x^2}$
解答
3Q_4H5参照(3Q_4H5の演習と同じ問題です)
2.次の関数のグラフの変曲点を求めよ。(分数関数については、漸近線も求めよ。)
(1) $y=\dfrac{1}{x^2+3}-\dfrac{5}{4}$
解答
定義:変曲点とは凹凸が変わる点、すなわち $y^{\prime\prime}$ の符号が変わる点
公式 $\left(\dfrac{1}{g}\right)^{\prime}=\dfrac{-g’}{g^2},\;\left(\dfrac{f}{g^n}\right)^{\prime}=\dfrac{f’g-nfg’}{g^{n+1}}$ を用いる
$\displaystyle \lim_{n\to \pm \infty}y=\displaystyle \lim_{n\to \pm \infty}\left(\dfrac{1}{x^2+3}-\dfrac{5}{4}\right)=\left(=\dfrac{1}{\infty}-\dfrac{5}{4}\right)-\dfrac{5}{4}$
従って、漸近線は $y=-\dfrac{5}{4}$ (答)
$y’=\dfrac{-2x}{(x^2+3)^2}\;\to\;y^{\prime\prime}=\dfrac{-2(x^2)+3-2(-2x)(2x)}{(x^2+3)^3}=\dfrac{6(x^2-1)}{(x^2+3)^3}$
$(y^{\prime\prime}\;の分子)=6(x^2-1)=0$ より $x=\pm 1$ だから、凹凸表を書くと次のようになる:
$\begin{array}{c|c c c c c}x&\cdots&-1&\cdots&1&\cdots \\ \hline y^{\prime\prime}&+&0&-&0&+ \\ y&下に凸&-1&上に凸&-1&下に凸\end{array}$
表より変曲点は $(\pm 1, -1)$ (答)
(2) $y=x+\mathrm{sin}x\;(0\lt x \lt 2\pi)$
解答
定義:変曲点とは凹凸が変わる点、すなわち $y^{\prime\prime}$ の符号が変わる点
$y’=1+\mathrm{cos}x\;\to\;y^{\prime\prime}=-\mathrm{sin}x=0\;\to\;\mathrm{sin}x=0\;(0\lt x \lt 2\pi)\;\to\;x=\pi$
従って、凹凸表を書くと次のようになる:
$\begin{array}{c|c c c c c}x&0&\cdots&\pi&\cdots&2\pi&\cdots \\ \hline y^{\prime\prime}&0&-&0&+&0 \\ y&0&上に凸&\pi&下に凸&2\pi\end{array}$
表より変曲点は $(\pi, \pi)$ (答)
成分表示と和・定数倍・内積
1.$\vec{a}=\begin{pmatrix}2\\2\\-3\end{pmatrix}$、$\vec{b}=\begin{pmatrix}1\\-2\\2\end{pmatrix}$ のとき $\vec{a}\cdot(3\vec{a}-2\vec{b})$ を求めよ。
解答
$\vec{a}\cdot(3\vec{a}-2\vec{b})=\begin{pmatrix}2\\2\\-3\end{pmatrix}\cdot\left\{3\begin{pmatrix}2\\2\\-3\end{pmatrix}-2\begin{pmatrix}1\\-2\\2\end{pmatrix}\right\}=\begin{pmatrix}2\\2\\-3\end{pmatrix}\cdot\left\{\begin{pmatrix}6\\6\\-9\end{pmatrix}-\begin{pmatrix}2\\-4\\4\end{pmatrix}\right\}$
$=\begin{pmatrix}2\\2\\-3\end{pmatrix}\cdot\begin{pmatrix}4\\10\\-13\end{pmatrix}=2\cdot4+2\cdot10+(-3)\cdot(-13)=67$ (答)
内積となす角
2.$\vec{a}=\begin{pmatrix}-2\\4\\-4\end{pmatrix}$、$\vec{b}=\begin{pmatrix}2\\-2\\0\end{pmatrix}$ のとき $\vec{a}$、$\vec{b}$ のなす角 $\theta\;(0\leqq \theta \leqq \pi)$ を求めよ。
解答
$\begin{matrix}\theta & 0^{\circ} & 30^{\circ} & 45^{\circ} & 60^{\circ} & 90^{\circ}\\ {\mathrm{cos}}\theta & 1& \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0 \end{matrix}$ $\hspace{20pt}$(公式) $\mathrm{Cos}^{-1}(-x)=\pi-\mathrm{Cos}^{-1}x$
(公式) ${\mathrm{cos}}\theta=\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}$ より $\theta={\mathrm{Cos}}^{-1}\left(\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\right)$ を用いる
$\vec{a}\cdot\vec{b}=(-2)\cdot2+4\cdot(-2)+(-4)\cdot 0=-12$、
$|\vec{a}|=\sqrt{2^2+4^2+(-4)^2}=6$、$|\vec{b}|=\sqrt{2^2+(-2)^2+0^2}=2\sqrt{2}$ よって、
$\theta={\mathrm{Cos}}^{-1}\left( \dfrac{-12}{6\cdot 2\sqrt{2}} \right)={\mathrm{Cos}}^{-1}\left(\dfrac{-\sqrt{2}}{2}\right)=\pi-{\mathrm{Cos}}^{-1}\left(\dfrac{\sqrt{2}}{2}\right)=\pi-\dfrac{\pi}{4}=\dfrac{3\pi}{4}$ (答)
分点の位置ベクトル
3.2点 $\mathrm{A}(5,5,1)$、$\mathrm{B}(1,-1,1)$ について、線分$\mathrm{AB}$ を$3:1$に外分する点$\mathrm{P}$ の座標を求めよ。
解答
外分なので、 $m:n=3:-1$ に分ける点として、分点の位置ベクトルの公式を用いる。
$\vec{p}=\dfrac{n\vec{a}+m\vec{b}}{m+n}=\dfrac{(-1)\vec{a}+3\vec{b}}{3+(-1)}=\dfrac{1}{2}\left(-\begin{pmatrix}5\\5\\1\end{pmatrix}+3\begin{pmatrix}1\\-1\\1\end{pmatrix}\right)$
$=\dfrac{1}{2}\begin{pmatrix}-2\\8\\2\end{pmatrix}=\begin{pmatrix}-1\\-4\\1\end{pmatrix}$ より $\mathrm{P}(-1,-4,1)$ (答)
平行条件・垂直条件
4. $\vec{a}=\begin{pmatrix}2\\x\\1\end{pmatrix}$、$\vec{b}=\begin{pmatrix}x\\y\\3\end{pmatrix}$ が平行であるように $x$、$y$ の値を定めよ。
解答
$\vec{a}, \vec{b}$ が平行だから、$\vec{b}=t\vec{a}\;(または、\vec{a}=t\vec{b})$ より
$\vec{b}=\begin{pmatrix}x\\y\\3\end{pmatrix}=t\vec{a}=t\begin{pmatrix}2t\\tx\\t\end{pmatrix}\;\Rightarrow\;\begin{cases}x=2t \\y=tx \\3=t
\end{cases}$ これを解いて
$t=3$ より $x=2t=2\cdot3=6, y=tx=3\cdot6=18$(答)
5.$\vec{a}=\begin{pmatrix}2\\x\\1\end{pmatrix}$、$\vec{b}=\begin{pmatrix}x\\1\\3\end{pmatrix}$ が垂直であるように $x$ の値を定めよ。
解答
$\vec{a}, \vec{b}$ が垂直だから、内積 $\vec{a}\cdot\vec{b}=0$ より
$\vec{a}\cdot\vec{b}=\begin{pmatrix}2\\x\\1\end{pmatrix}\cdot\begin{pmatrix}x\\1\\3\end{pmatrix}=2\cdot x+x\cdot 1 +1\cdot 3=3x+3=0$ より $x=-1$ (答)
球面の方程式
6. 点 $(1,-2,1)$ を中心とする、半径 $\sqrt{6}$ の球面の方程式の一般形を求めよ。
解答
中心 $(a, b, c)$ 半径 $r$ の球面の方程式: $(x-a)^2+(y-b)^2+(z-c)^2=r^2$ を用いる
$(x-1)^2+(y+2)^2+(z-1)^2=(\sqrt{6})^2$ だから、一般形はこれを展開して
$x^2+y^2+z^2-2x+4y-2z=0$ (答)
7. 方程式 $x^2+y^2+z^2-4x+2y-2z+1=0$ で表される球面の中心と半径を求めよ。
解答
平方完成して標準形にすると $\underbrace{x^2-4x}_{(x-2)^2-4}+\underbrace{y^2+2y}_{(y+1)^2-1}+\underbrace{z^2-2z}_{(z-1)^2-1}+1=0\; \to\; (x-2)^2+(y+1)^2+(z-1)^2=5$ より
中心 $(2, -1, 1)$ 半径 $\sqrt{5}$ (答)
不定積分(基本)
1. 次の不定積分を求めよ。
(1) $\displaystyle \int \left(x^2+2x+\dfrac{3}{x}+\dfrac{2}{x^3}\right) \,dx$
解答
公式$\displaystyle \int x^n \,dx = \dfrac{1}{n+1}x^{n+1}+C\;(n\neq -1),\;\displaystyle \int \dfrac{1}{x} \,dx =\mathrm{log}|x|+C$ を用いる
$\displaystyle \int \left(x^2+2x+\dfrac{3}{x}+2x^{-3}\right) \,dx=\dfrac{1}{3}x^3+x^2+3\mathrm{log}|x|-\dfrac{1}{x^2}+C$ (答)
(2) $\displaystyle \int (5x-3)^7 \,dx$
解答
公式 $\displaystyle \int (ax+b)^n \,dx = \dfrac{1}{a(n+1)}(ax+b)^{n+1}+C\;(n\neq-1)$ を用いる
$\displaystyle \int (5x-3)^7 \,dx=\dfrac{1}{5\cdot8}(5x-3)^8+C=\dfrac{1}{40}(5x-3)^8+C$ (答)
(3) $\displaystyle \int \dfrac{1}{\sqrt[5]{4x+7}} \,dx$
解答
公式 $\displaystyle \int (ax+b)^n \,dx =\dfrac{1}{a} \cdot \dfrac{1}{n+1} (ax+b)^{n+1}+C\;(n\neq -1)$ を用いる
$\displaystyle \int (4x+7)^{\tiny{\dfrac{-1}{5}}} \,dx=\dfrac{1}{4}\dfrac{5}{4}(4x+7)^{\tiny{\dfrac{4}{5}}}+C=\dfrac{5}{16}\sqrt[5]{(4x+t)^4}$ (答)
(4) $\displaystyle \int \mathrm{sin}(7x-2) \,dx$
解答
公式 $\displaystyle \int \mathrm{sin}(ax+b) \,dx =-\dfrac{1}{a} \mathrm{cos}(ax+b)+C$
$\hspace{20pt}\displaystyle \int \mathrm{cos}(ax+b) \,dx =\dfrac{1}{a} \mathrm{sin}(ax+b)+C$ 等を用いる
$\displaystyle \int \mathrm{sin}(7x-2) \,dx=-\dfrac{1}{7}\mathrm{cos}(7x-2)+C$ (答)
(5) $\displaystyle \int e^{-2x+3} \,dx$
解答
公式 $\displaystyle \int e^{ax+b} \,dx=\dfrac{1}{a}e^{ax+b}+C$ を用いる
$\displaystyle \int e^{-2x+3} \,dx=\dfrac{-1}{2}e^{-2x+3}+C$ (答)
(6) $\displaystyle \int \dfrac{1}{\mathrm{cos}^2(4x+1)} \,dx$
解答
公式 $\displaystyle \int \dfrac{1}{\mathrm{cos}^2(ax+b)} \,dx=\dfrac{1}{a}\mathrm{tan}(ax+b)+C$ を用いる
$\displaystyle \int \dfrac{1}{\mathrm{cos}^2(4x+1)} \,dx=\dfrac{1}{4}\mathrm{tan}(4x+1)+C$ (答)
(7) $\displaystyle \int \dfrac{\mathrm{cos}x}{5+\mathrm{sin}x} \, dx$
解答
公式 $\displaystyle \int \dfrac{f’}{f} \, dx=\mathrm{log}|f|+C$ を用いる
$\displaystyle \int \dfrac{\mathrm{cos}x}{5+\mathrm{sin}x} \, dx=\displaystyle \int \dfrac{(5+\mathrm{sin}x)^{\prime}}{5+\mathrm{sin}x} \, dx=\mathrm{log}|5+\mathrm{sin}x|+C$ (答)
(8) $\displaystyle \int \dfrac{x^4}{x^5-5} \,dx$
解答
公式 $\displaystyle \int \dfrac{f’}{f} \, dx=\mathrm{log}|f|+C$ を用いる
$\displaystyle \int \dfrac{x^4}{x^5-5} \,dx=\dfrac{1}{5}\displaystyle \int \dfrac{5x^4}{x^5-5} \,dx=\dfrac{1}{5}\displaystyle \int \dfrac{(x^5-5)’}{x^5-5} \,dx=\dfrac{1}{5}\mathrm{log}|x^5-5|+C$ (答)
不定積分(三角関数の公式を利用する問題)
2.次の不定積分を求めよ。
(1) $\displaystyle \int \mathrm{tan}x \,dx$
解答
公式 $\;\mathrm{tan}x=\dfrac{\mathrm{sin}x}{\mathrm{cos}x},\;\mathrm{cot}x=\dfrac{\mathrm{cos}x}{\mathrm{sin}x}\;$ 等を用いる
$\displaystyle \int \mathrm{tan}x \,dx=-\displaystyle \int \dfrac{-\mathrm{sin}x}{\mathrm{cos}x} \,dx=-\displaystyle \int \dfrac{(\mathrm{cos}x)’}{\mathrm{cos}x} \,dx=-\mathrm{log}|\mathrm{cos}x|+C$ (答)
(2) $\displaystyle \int \mathrm{tan}^2x \,dx$
解答
公式 $\;\mathrm{tan}^2x=\dfrac{1}{\mathrm{cos}^2x}-1,\;\mathrm{cot}^2x=\dfrac{1}{\mathrm{sin}^2x}-1\;$ 等を用いる
$\displaystyle \int \mathrm{tan}^2x \,dx=\displaystyle \int \left(\dfrac{1}{\mathrm{cos}^2x}-1\right) \,dx=\mathrm{tan}x-x+C$ (答)
(3) $\displaystyle \int \mathrm{cos}7x\,\mathrm{cos}3x \,dx$
解答
公式 $\;\mathrm{cos}\alpha\,\mathrm{cos}\beta=\dfrac{1}{2}\left(\mathrm{cos}(\alpha+\beta)+\mathrm{cos}(\alpha-\beta)\right)$
$\hspace{22pt} \mathrm{sin}\alpha \,\mathrm{cos}\beta=\dfrac{1}{2}\left(\mathrm{sin}(\alpha+\beta)+\mathrm{sin}(\alpha-\beta)\right)$
$\hspace{22pt}\mathrm{sin}\alpha \,\mathrm{sin}\beta=\dfrac{-1}{2}\left(\mathrm{cos}(\alpha+\beta)-\mathrm{cos}(\alpha-\beta)\right)\;$ 等を用いる
$\displaystyle \int \mathrm{cos}7x\,\mathrm{cos}3x \,dx=\dfrac{1}{2}\displaystyle \int (\mathrm{cos}10x+\mathrm{cos}4x) \,dx$
$=\dfrac{1}{2}\left(\dfrac{1}{10}\mathrm{sin}10x + \dfrac{1}{4}\mathrm{sin}4x \right)+C=\dfrac{1}{20}\mathrm{sin}10x+\dfrac{1}{8}\mathrm{sin}4x +C$ (答)
(4) $\displaystyle \int \mathrm{sin}^2x \,dx$
解答
公式 $\;\mathrm{sin}^2x=\dfrac{1}{2}(1-\mathrm{cos}2x),\;\mathrm{cos}^2x=\dfrac{1}{2}(1+\mathrm{cos}2x)\;$ 等を用いる
$\displaystyle \int \mathrm{sin}^2x \,dx=\dfrac{1}{2}\displaystyle \int (1-\mathrm{cos}2x) \,dx=\dfrac{1}{2}\left(x-\dfrac{1}{2}\mathrm{sin}2x\right)+C=\dfrac{1}{2}x-\dfrac{1}{4}\mathrm{sin}2x+C$ (答)
不定積分(部分積分)
1.次の不定積分を求めよ。
(1) $I=\displaystyle \int (3x+1)e^{2x+1} \,dx$
解答

$I=(3x+1)\cdot\dfrac{2}{4}e^{2x+1}-3\cdot\dfrac{1}{4}e^{2x+1}+C=\dfrac{6x+2-3}{4}e^{2x+1}+C$
$\quad =\dfrac{(6x-1)e^{2x+1}}{4}+C$ (答) (2) $I=\displaystyle \int x^2\mathrm{cos}(2x+3) \,dx$
解答
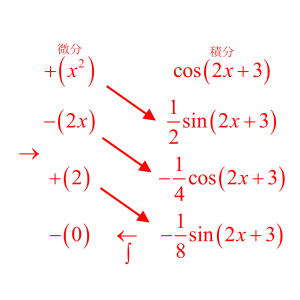
$I=\dfrac{1}{2}x^2\mathrm{sin}(2x+3)+\dfrac{1}{2}x\mathrm{cos}(2x+3)-\dfrac{1}{4}\mathrm{sin}(2x+3)+C$ (答) (3) $I=\displaystyle \int (2x+1)^3\mathrm{log}(2x+1) \,dx$
解答
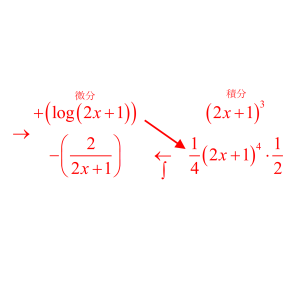
$I=\dfrac{1}{8}(2x+4)^4\mathrm{log}(2x+1)-\dfrac{1}{4}\displaystyle \int (2x+1)^3 \,dx$
$\quad =\dfrac{1}{8}(2x+4)^4\mathrm{log}(2x+1)-\dfrac{1}{4}\cdot\dfrac{1}{2\cdot4}(2x+1)^4+C$
$\quad =\dfrac{1}{8}(2x+4)^4\mathrm{log}(2x+1)-\dfrac{1}{32}(2x+1)^4+C$ (答) (4) $I=\displaystyle \int e^{3x}\mathrm{cos}2x \,dx$
解答
$\displaystyle \int e^{ax}\mathrm{cos}bx \,dx=\dfrac{e^{ax}}{a^2+b^2}(a\mathrm{cos}bx+b\mathrm{sin}bx)+C$
$\displaystyle \int e^{ax}\mathrm{sin}bx \,dx=\dfrac{e^{ax}}{a^2+b^2}(a\mathrm{sin}bx-b\mathrm{cos}bx)+C$ 等を用いる
$I=\dfrac{e^{3x}}{3^2+2^2}(3\mathrm{cos}2x+2\mathrm{sin}2x)+C$ (答)
不定積分(置換積分)
2.次の不定積分を求めよ。
(1) $I=\displaystyle \int \mathrm{sin}^5x\mathrm{cos}x \,dx$
解答
$t=\mathrm{sin}x\;\to\;dt=\mathrm{cos}xdx$ より
$I=\displaystyle \int t^5 \,\underset{\mathrm{cos}xdx}{dt}=\dfrac{1}{6}t^6+C=\dfrac{1}{6}\mathrm{sin}^6x$ (答)
(2) $I=\displaystyle \int \dfrac{\mathrm{cos}x}{\mathrm{sin}^5x} \,dx$
解答
$t=\mathrm{sin}x\;\to\;dt=\mathrm{cos}xdx$ より
$I=\displaystyle \int \dfrac{1}{t^5} \,\underset{\mathrm{cos}xdx}{dt}=\displaystyle \int t^{-5} \,dt=\dfrac{1}{-4}t^{-4}+C=\dfrac{-1}{4t^4}+C=\dfrac{-1}{4\mathrm{sin}^4x}+C$ (答)
(3) $I=\displaystyle \int \dfrac{\mathrm{log}x}{x} \,dx$
解答
$t=\mathrm{log}x\;\to\;dt=\dfrac{1}{x}dx$ より
$I=\displaystyle \int t \,\underset{{\scriptsize \dfrac{1}{x}}dx}{dt}=\dfrac{1}{2}t^2+C=\dfrac{1}{2}(\mathrm{log}x)^2+C$ (答)
(4) $I=\displaystyle \int (2x+1)(x^2+x+1)^5 \,dx$
解答
$t=x^2+x+1\;\to\;dt=(2x+1)dx$ より
$I=\displaystyle \int t^5 \,\underset{(2x+1)dx}{dt}=\dfrac{1}{6}t^6+C=\dfrac{1}{6}(x^2+x+1)^6+C$ (答)
(5) $I=\displaystyle \int \dfrac{x}{\sqrt{x^2+1}} \,dx$
解答
$t=x^2+1\;\to\;dt=2xdx$ より
$I=\dfrac{1}{2}\displaystyle \int \dfrac{2x}{\sqrt{x^2+1}} \,dx=\dfrac{1}{2}\displaystyle \int \dfrac{1}{\sqrt{t}} \;\underset{2xdx}{dt}=\dfrac{1}{2}\displaystyle \int t^{\tiny\dfrac{-1}{2}} \,dt$
$\quad =\dfrac{1}{2}\cdot\dfrac{2}{1}t^{\tiny\dfrac{1}{2}}+C=\sqrt{t}+C=\sqrt{x^2+1}+C$ (答)
直線の方程式
1. 2点 ${\mathrm{A}}(1,-5,2), {\mathrm{B}}(3,-3,5)$ を通る直線の方程式を求めよ。
解答
方向ベクトルは $\vec{v}=\overrightarrow{\mathrm{AB}}=\overset{B-A}{\begin{pmatrix}3-1\\-3-(-5)\\5-2\end{pmatrix}}=\begin{pmatrix}2\\2\\3\end{pmatrix}$ で、点 $\mathrm{A}(1,-5,2)$ を通るので、
$\dfrac{x-1}{2}=\dfrac{y+5}{2}=\dfrac{z-2}{3}$(答)
平面の方程式
2. 点 ${\mathrm{A}}(1,-5,2)$ を通り、直線 $\dfrac{x+1}{3}=\dfrac{y-2}{2}=\dfrac{z-3}{-3}$ に垂直な平面方程式を求めよ。
解答
直線の方向ベクトルが求める平面の法線ベクトル $\vec{n}=\begin{pmatrix}3\\2\\-3\end{pmatrix}$ だから、点 ${\mathrm{A}}(1,-1,3)$ を通るので、
$3(x-1)+2(y+1)-3(z-3)=0$ より、展開して、$3x+2y-3z+8=0$ (答)
3点を通る平面の方程式
3. 3点 ${\mathrm{A}}(2,2,-2), {\mathrm{B}}(2,3,1), {\mathrm{C}}(5,2,-1)$ を通る平面の法線ベクトル $\vec{n}$ を求めよ。
解答
$\overrightarrow{\mathrm{AB}}=\overset{B-A}{\begin{pmatrix}2-2\\3-2\\1-(-2)\end{pmatrix}}=\begin{pmatrix}0\\1\\3\end{pmatrix},\;\overrightarrow{\mathrm{AC}}=\overset{C-A}{\begin{pmatrix}5-2\\2-2\\-1-(-2)\end{pmatrix}}=\begin{pmatrix}3\\0\\1\end{pmatrix}$ また、$\vec{n}=\begin{pmatrix}1\\a\\b\end{pmatrix}$ とおくと
$\vec{n}\cdot\overrightarrow{\mathrm{AB}}=a+3b=0,\;\vec{n}\cdot\overrightarrow{\mathrm{AC}}=3+b=0$ より $a=9,\;b=-3$ だから、$\vec{n}=\begin{pmatrix}1\\9\\-3\end{pmatrix}$ (答)
(別解) $\vec{n}=\overrightarrow{\mathrm{AB}}\times\overrightarrow{\mathrm{AC}}=\begin{pmatrix}0\\1\\3\end{pmatrix}\times\begin{pmatrix}3\\0\\1\end{pmatrix}=\begin{pmatrix}\begin{vmatrix}
1 & 0 \\
3 & 1
\end{vmatrix}\\-\begin{vmatrix}
0 & 3 \\
3 & 1
\end{vmatrix}\\\begin{vmatrix}
0 & 3 \\
1 & 0
\end{vmatrix}\end{pmatrix}=\begin{pmatrix}1\\-(-9)\\-3\end{pmatrix}=\begin{pmatrix}1\\9\\-3\end{pmatrix} $ (答)
点と平面の距離
4.点 $(2,1,0)$ と平面 $2x-y+2z+1=0$ との距離 $h$ を求めよ。
解答
点 $(x_0, y_0, z_0)$ と平面 $ax+by+cz+d=0$ との距離を $h$ とするとき
公式 $h=\dfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}$ を用いる
$h=\dfrac{|2\cdot2-1+2\cdot0+1|}{\sqrt{2^2+(-1)^2+2^2}}=\dfrac{|4|}{\sqrt{9}}=\dfrac{4}{3}$ (答)
直線と平面の交点
5.直線 $\dfrac{x+1}{3}=\dfrac{y-2}{2}=\dfrac{z-3}{-3}$ と平面 $2x-y+2z+6=0$ の交点 $\mathrm{P}$ を求めよ。
解答
$\dfrac{x+1}{3}=\dfrac{y-2}{2}=\dfrac{z-3}{-3}=t$ とおくと
$x=3t-1, y=2t-2, z=2t+1\cdots(*)$ より、平面の方程式に代入して
$2(3t-1)-(2t-2)+2(2t+1)+6=0\;\to\;8t+8=0\;\to\;t=-1$ これを $(*)$ に代入して
$x=3(-1)-1=-4, y=2(-1)-2=-4, z=2(-1)+1=-1$ より
交点は $\mathrm{P}(-4, -4, -1)$ (答)