数学II_2Q2H_1

        Next
        再生リスト
テキスト 演習 演習解答 課題 解説
2Q2H_1 2Q2H_E1 2Q2H_ES1 2Q2H_K1 2Q2H_V1
$a^→+b^→=?$、$a^→-b^→=?$、$ca^→=?$、 $|a^→|=?$
$\vec{a}+\vec{b}=$(矢印を繋いで、始点と終点を結ぶ)
$\vec{a}-\vec{b}=$($\vec{a}$と$\vec{b}$の逆ベクトル$-\vec{b}$をたす)
$c\vec{a}=$($c>0$の時は、$c$倍する、$c<0$の時は、逆向きに$|c|$倍する)
$|\vec{a}|=$(矢印の長さ)

Targets
1. ベクトル $\vec{a},\vec{b}$を与えて、
$\quad$ベクトルの線形和　$\vec{c}=\alpha\vec{a}+\beta\vec{b}$ を作図することができる
$\quad$また、ベクトルの大きさ $\left|\vec{c}\right|$を求めることができる
2. 正六角形・三角形または立方体の
$\quad$平行でない2辺に向きを付けたベクトル $\vec{a},\vec{b}$ を与えて、任意の頂点を
$\quad$結んでできるベクトル $\vec{c}$ を $\vec{a},\vec{b}$ を用いて表すことができる
2Q2H_2 2Q2H_E2 2Q2H_ES2 2Q2H_K2 2Q2H_V2
        2Q2H_pf2
内積 $a^→$・$b^→=?$、線分の交点$P$と始点$O$を結ぶベクトル$OP^→=?$
$\vec{a}\cdot\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|{\mathrm{cos}} \theta \quad$ ($\theta$ はベクトル $\vec{a}, \vec{b}$ のなす角)

直線 ${\mathrm{AB}}$ 上の点 ${\mathrm{P}}$

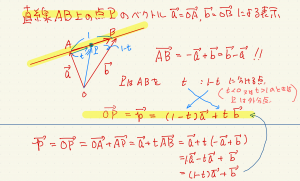
ベクトル $\vec{a}, \vec{b}$ が平行でないとき
$\alpha_1\vec{a}+\beta_1\vec{b}=\alpha_2\vec{a}+\beta_2\vec{b} \; \Rightarrow \; \alpha_1=\alpha_2, \; \beta_1=\beta_2$

（参考）メネラウスの定理

Targets
1. 各辺の長さが $l$ の立方体を与えて、各頂点を結んでできるベクトルの内積
$\quad$を求めることができる
2. 三角形 $\triangle {\mathrm{OAB}}$ とベクトル $\overrightarrow{\mathrm{OA}}=\vec{a},\;\overrightarrow{\mathrm{OB}}=\vec{b}$ および2辺の内分点 $\mathrm{C}, \mathrm{D}$
$\quad$を与えて、線分${\mathrm{AD}}$ と ${\mathrm{BC}}$ の交点を $\mathrm{P}$ とするとき、
$\quad$ベクトル$\overrightarrow{\mathrm{OP}}$ を $\vec{a}, \vec{b}$ を用いてあらわすことができる
2Q2H_3 2Q2H_E3 2Q2H_ES3 2Q2H_K3 2Q2H_V3
        2Q2H_pf3
$a^→, b^→$　の成分表示が与えられたとき 　$|a^→|=?$、$pa^→+qb^→=?$、$a^→$・$b^→=?$
$\vec{a}=\begin{pmatrix}a_1 \\ a_2 \end{pmatrix}$、$\vec{b}=\begin{pmatrix}b_1 \\ b_2 \end{pmatrix}$ のとき $|\vec{a}|=\sqrt{a_1^2+a_2^2}$、$|\vec{b}|=\sqrt{b_1^2+b_2^2}$
$p\vec{a}+q\vec{b}=\begin{pmatrix}pa_1+qb_1 \\ pa_2+qb_2 \end{pmatrix}$、$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2$、$\vec{a}\cdot\vec{a}=a_1^2+a_2^2=|\vec{a}|^2$
$\vec{a}, \vec{b}$ のなす角を $\theta$ とすると、$\theta={\mathrm{cos}}^{-1}\dfrac{\vec{a}\cdot\vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right|}$
Targets
1. 座標平面上にベクトルを与えて、成分表示と大きさを求めることができる
2. ベクトル $\vec{a}, \vec{b}$ の成分表示が与えられたとき次が計算できる
$\quad$線形和 $p\vec{a}+q\vec{b}=?$、 大きさ $|\vec{a}|=?$、 内積 $\vec{a}\cdot\vec{b}=?$
3. $|\vec{a}|$ と $\left|\vec{b}\right|$ がわかっているとき、
$\quad$$\left| \vec{a}\pm \vec{b} \right| \Rightarrow \vec{a}\cdot\vec{b}=?$、$ \vec{a}\cdot\vec{b}　\Rightarrow \left|\vec{a}\pm \vec{b} \right|=?$
        Next