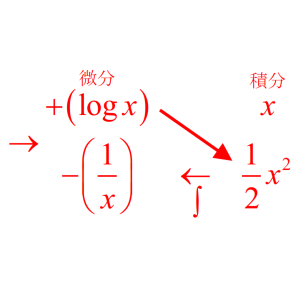不定積分:公式 II
1.次の不定積分を求めよ。
(1) $\displaystyle\int\dfrac{1}{x^2+25}\,dx$
解答
公式 $\displaystyle\int\dfrac{1}{x^2+a^2}\,dx=\dfrac{1}{a}\mathrm{Tan}^{-1}\dfrac{x}{a}+C\;(a\gt 0)$ を用いる
$\displaystyle\int\dfrac{1}{x^2+25}\,dx=\dfrac{1}{5}\mathrm{Tan}^{-1}\dfrac{x}{5}+C$ (答)
(2) $\displaystyle\int\dfrac{1}{x^2-25}\,dx$
解答
公式 $\displaystyle\int\dfrac{1}{x^2-a^2}\,dx=\dfrac{1}{2a}\mathrm{log}\left|\dfrac{x-a}{x+a}\right|+C\;(a\gt 0)$ を用いる
$\displaystyle\int\dfrac{1}{x^2-25}\,dx=\dfrac{1}{10}\mathrm{log}\left|\dfrac{x-5}{x+5}\right|+C$ (答)
(3) $\displaystyle\int\dfrac{1}{\sqrt{x^2+25}}\,dx$
解答
公式 $\displaystyle\int\dfrac{1}{\sqrt{x^2+A}}\,dx=\mathrm{log}\left|x+\sqrt{x^2+A}\right|+C\;(A\neq 0)$ を用いる
$\displaystyle\int\dfrac{1}{\sqrt{x^2+25}}\,dx=\mathrm{log}\left|x+\sqrt{x^2+25}\right|+C$ (答)
(4) $\displaystyle\int\dfrac{1}{\sqrt{25-x^2}}\,dx$
解答
公式 $\displaystyle\int\dfrac{1}{\sqrt{a^2-x^2}}\,dx=\mathrm{Sin}^{-1}\dfrac{x}{a}+C\;(a\gt 0)$ を用いる
$\displaystyle\int\dfrac{1}{\sqrt{25-x^2}}\,dx=\mathrm{Sin}^{-1}\dfrac{x}{5}+C$ (答)
(5) $\displaystyle\int\dfrac{1}{\sqrt{x^2-25}}\,dx$
解答
公式 $\displaystyle\int\dfrac{1}{\sqrt{x^2+A}}\,dx=\mathrm{log}\left|x+\sqrt{x^2+A}\right|+C\;(A\neq 0)$ を用いる
$\displaystyle\int\dfrac{1}{\sqrt{x^2-25}}\,dx=\mathrm{log}\left|x+\sqrt{x^2-25}\right|+C$ (答)
(6) $\displaystyle\int\sqrt{x^2+25}\,dx$
解答
公式 $\displaystyle\int\sqrt{x^2+A}\,dx=\dfrac{1}{2}\left(x\sqrt{x^2+A}+A\mathrm{log}\left|x+\sqrt{x^2+A}\right|\right)+C\;(A\neq 0)$ を用いる
$\displaystyle\int\sqrt{x^2+25}\,dx=\dfrac{1}{2}\left(x\sqrt{x^2+25}+25\mathrm{log}\left|x+\sqrt{x^2+25}\right|\right)+C$ (答)
(7) $\displaystyle\int\sqrt{25-x^2}\,dx$
解答
公式 $\displaystyle\int\sqrt{a^2-x^2}\,dx=\dfrac{1}{2}\left(x\sqrt{a^2-x^2}+a^2\mathrm{Sin}^{-1}\dfrac{x}{a}\right)+C\;(a\gt 0)$ を用いる
$\displaystyle\int\sqrt{25-x^2}\,dx=\dfrac{1}{2}\left(x\sqrt{25-x^2}+25 \mathrm{Sin}^{-1}\dfrac{x}{5}\right)+C$ (答)
(8) $I=\displaystyle\int\dfrac{1}{x^2+2x+5}\,dx$
解答
公式 $\displaystyle\int\dfrac{1}{(ax+b)^2+c^2}\,dx=\dfrac{1}{ac}\mathrm{Tan}^{-1}\dfrac{ax+b}{c}+C\;(c\gt 0, a\neq 0)$ を用いる
$I=\displaystyle\int\dfrac{1}{(x^2+2x+1)-1+5}\,dx=\displaystyle\int\dfrac{1}{(x+1)^2+4}\,dx=\dfrac{1}{2}\mathrm{Tan}^{-1}\dfrac{x+1}{2}+C$ (答)
(9) $I=\displaystyle\int\dfrac{1}{x^2+2x-3}\,dx$
解答
公式 $\displaystyle\int\dfrac{1}{(ax+b)^2-c^2}\,dx=\dfrac{1}{2ac}\mathrm{log}\left|\dfrac{(ax+b)-c}{(ax+b)+c}\right|+C\;(c\gt 0, a\neq 0)$ を用いる
$I=\displaystyle\int\dfrac{1}{(x^2+2x+1)-1-3}\,dx=\displaystyle\int\dfrac{1}{(x+1)^2-4}\,dx$
$\quad=\dfrac{1}{2\cdot1\cdot2}\mathrm{log}\left|\dfrac{(x+1)-2}{(x+1)+2}\right|+C=\dfrac{1}{4}\mathrm{log}\left|\dfrac{x-1}{x+3}\right|+C$ (答)
(10) $I=\displaystyle\int\dfrac{1}{\sqrt{x^2+2x+5}}\,dx$
解答
公式 $\displaystyle\int\dfrac{1}{\sqrt{(ax+b)^2+A}}\,dx=\dfrac{1}{a}\mathrm{log}\left|ax+b+\sqrt{(ax+b)^2+A}\right|+C\;(A, a\neq 0)$
$I=\displaystyle\int\dfrac{1}{\sqrt{(x^2+2x+1)-1+5}}\,dx=\displaystyle\int\dfrac{1}{\sqrt{(x+1)^2+4}}\,dx$
$\quad=\dfrac{1}{1}\mathrm{log}\left|(x+1)+\sqrt{(x+1)^2+4}\right|+C=\mathrm{log}\left|x+1+\sqrt{x^2+2x+5}\right|+C$ (答)
(11) $I=\displaystyle\int\dfrac{1}{\sqrt{3-x^2-2x}}\,dx$
解答
公式 $\displaystyle\int\dfrac{1}{\sqrt{c^2-(ax+b)^2}}\,dx=\dfrac{1}{a}\mathrm{Sin}^{-1}\dfrac{ax+b}{c}+C\;(c\gt 0, a\neq0)$ を用いる
$I=\displaystyle\int\dfrac{1}{\sqrt{3+1-(x^2+2x+1)}}\,dx=\displaystyle\int\dfrac{1}{\sqrt{4-(x+1)^2}}\,dx=\mathrm{Sin}^{-1}\dfrac{x+1}{2}+C$ (答)
不定積分:部分分数分解
2.次の不定積分を求めよ。
(1) $I=\displaystyle\int\dfrac{5}{(x-1)(x+3)}\,dx$
解答
$\dfrac{5}{(x-1)(x+3)}=\dfrac{a}{x-1}+\dfrac{b}{x+3}=\dfrac{(a+b)x+3a-b}{(x-1)(x+3)}$ より
$a+b=0, 3a-b=5 \Rightarrow a=\dfrac{5}{4}, b=-\dfrac{5}{4}$ だから
$I=\dfrac{5}{4}\displaystyle\int\left(\dfrac{1}{x-1}-\dfrac{1}{x+3}\right)\,dx=\dfrac{5}{4}\underbrace{\mathrm{log}\left|\dfrac{x-1}{x+3}\right|}_{\mathrm{log}|x-1|-\mathrm{log}|x+3|}+C$ (答)
(2) $I=\displaystyle\int\dfrac{9x-4}{(3x+1)(x-2)}\,dx$
解答
$\dfrac{9x-4}{(3x+1)(x-2)}=\dfrac{a}{3x+1}+\dfrac{b}{x-2}=\dfrac{(a+3b)x-2a+b}{(3x+1)(x-2)}$ より
$a+3b=9, -2a+b=-4 \Rightarrow a=3, b=2$ だから
$I=\displaystyle\int\left(\dfrac{3}{3x+1}+2\cdot\dfrac{1}{x-2}\right)\,dx=\underbrace{\mathrm{log}|3x+1|(x-2)^2}_{\mathrm{log}|3x+1|+2\mathrm{log}|x-2|}+C$ (答)
(3) $I=\displaystyle\int\dfrac{x^2+3x}{(x^2+1)(x+1)}\,dx$
解答
$\dfrac{x^2+3x}{(x^2+1)(x+1)}=\dfrac{ax+b}{x^2+1}+\dfrac{c}{x+1}=\dfrac{(a+c)x^2+(a+b)x+(b+c)}{(x^2+1)(x+1)}$ より
$a+c=1, a+b=3, b+c=0 \Rightarrow a=2, b=1, c=-1$ だから
$I=\displaystyle\int\left(\dfrac{2x+1}{x^2+1}-\dfrac{1}{x+1}\right)\,dx=\displaystyle\int\left(\dfrac{1}{x^2+1}+\dfrac{2x}{x^2+1}-\dfrac{1}{x+1}\right)\,dx$
$\quad=\mathrm{Tan}^{-1}x+\underbrace{\mathrm{log}\dfrac{x^2+1}{|x+1|}}_{\mathrm{log}(x^2+1)-\mathrm{log}|x-1|}+C$ (答)
(4) $I=\displaystyle\int\dfrac{x-3}{(x-1)^2(x+1)}\,dx$
解答
$\dfrac{x-3}{(x-1)^2(x+1)}=\dfrac{a}{(x-1)^2}+\dfrac{b}{x-1}+\dfrac{c}{x+1}=\dfrac{(b+c)x^2+(a-2c)x+(a-b+c)}{(x-1)^2(x+1)}$
より $b+c=0, a-2c=1, a-b+c=3 \Rightarrow a=-1, b=1, c=-1$ だから
$I=\displaystyle\int\left(\dfrac{-1}{(x-1)^2}+\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\,dx=\displaystyle\int\left(-(x-1)^{-2}+\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\,dx$
$=\underbrace{\dfrac{1}{x-1}}_{\dfrac{-1}{-1}(x-1)^{-1}}+\underbrace{\mathrm{log}\left|\dfrac{x-1}{x+1}\right|}_{\mathrm{log}|x-1|-\mathrm{log}|x+1|}+C$ (答)
不定積分:三角関数の有理式
1.次の不定積分を求めよ。
(1) $I=\displaystyle\int\dfrac{1}{2\mathrm{cos}x+3\mathrm{sin}x+2}\,dx$
解答
$u=\mathrm{tan}\dfrac{x}{2} \Rightarrow \mathrm{cos}x=\dfrac{1-u^2}{1+u^2}, \mathrm{sin}x=\dfrac{2u}{1+u^2}, dx=\dfrac{2}{1+u^2}du$ より
$I=\displaystyle\int\dfrac{1}{\left(2\cdot\dfrac{1-u^2}{1+u^2}+3\cdot\dfrac{2u}{1+u^2}+2 \right)}\dfrac{2}{1+u^2}\,du$
$\quad=\displaystyle\int\underbrace{\dfrac{2}{2\cdot(1-u^2)+3\cdot 2u+2(1+u^2)}}_{4+6u=2(3u+2)}\,du$
$\quad=\displaystyle\int\dfrac{1}{3u+2}\,du=\dfrac{1}{3}\displaystyle\int\dfrac{3}{3u+2}\,du=\dfrac{1}{3}\mathrm{log}|3u+2|+C=\dfrac{1}{3}\mathrm{log}|3 \mathrm{tan}\dfrac{x}{2}+2|+C$ (答)
(2) $I=\displaystyle\int\dfrac{1}{\mathrm{cos}x+2\mathrm{sin}x+3}\,dx$
解答
$u=\mathrm{tan}\dfrac{x}{2} \Rightarrow \mathrm{cos}x=\dfrac{1-u^2}{1+u^2}, \mathrm{sin}x=\dfrac{2u}{1+u^2}, dx=\dfrac{2}{1+u^2}du$ より
$I=\displaystyle\int\dfrac{1}{\left(\dfrac{1-u^2}{1+u^2}+2\cdot\dfrac{2u}{1+u^2}+3 \right)}\dfrac{2}{1+u^2}\,du$
$\quad=\displaystyle\int\underbrace{\dfrac{2}{(1-u^2)+2\cdot 2u+3(1+u^2)}}_{2u^2+4u+4=2(u^2+2u+2)=2\{(u+1)^2+1\}}\,du$
$\quad=\displaystyle\int\dfrac{1}{(u+1)^2+1}\,du=\mathrm{Tan}^{-1}(u+1)+C=\mathrm{Tan}^{-1}\left(\mathrm{tan}\dfrac{x}{2}+1\right)+C$ (答)
定積分:偶関数と奇関数
2.次の定積分の値を求めよ。
(1) $I=\displaystyle\int_{-2}^{2}(x^5-2x^3+3x^2+5x+1)\,dx$
解答
$x^5-2x^3+5x$は奇関数だから、$\displaystyle\int_{-2}^{2}(x^5-2x^3+5x)\,dx=0$ また、$3x^2+1$ は偶関数だから
$I=\displaystyle\int_{-2}^{2}(3x^2+1)\,dx=2\displaystyle\int_{0}^{2}(3x^2+1)\,dx=2\lbrack x^3+x \rbrack_{0}^{2}=2(8+2)=20$ (答)
(2) $I=\displaystyle\int_{-1}^{1}\dfrac{x\mathrm{cos}x+1}{x^2+1}\,dx$
解答
$I=\displaystyle\int_{-1}^{1}\dfrac{x\mathrm{cos}x}{x^2+1}\,dx+\displaystyle\int_{-1}^{1}\dfrac{1}{x^2+1}\,dx$ ここで、$f(x)=\dfrac{x\mathrm{cos}x}{x^2+1}$ とおくと、
$f(x)=\dfrac{x\mathrm{cos}x}{x^2+1} \Rightarrow f(-x)=\dfrac{-x\mathrm{cos}(-x)}{(-x)^2+1}=\dfrac{-x\mathrm{cos}x}{x^2+1}=-f(x) $ より奇関数だから、
$\displaystyle\int_{-1}^{1}\dfrac{x\mathrm{cos}x}{x^2+1}\,dx=0$ また、$\dfrac{1}{x^2+1}$ は偶関数だから、
$I=\displaystyle\int_{-1}^{1}\dfrac{1}{x^2+1}\,dx=2\displaystyle\int_{0}^{1}\dfrac{1}{x^2+1}\,dx=2\left\lbrack \mathrm{Tan}^{-1}x \right\rbrack _0^1 =2(\underbrace{\mathrm{Tan}^{-1}1}_{\scriptsize \dfrac{\pi}{4}}-0)=\dfrac{\pi}{2}$
定積分:基本
3.次の定積分の値を求めよ。
(1) $I=\displaystyle\int_{-2}^{1}x^2\,dx$
解答
$I=\dfrac{1}{3}\left\lbrack x^3 \right\rbrack_{-2}^{1}=\dfrac{1}{3}\left\lbrace 1^3 -(-2)^3 \right \rbrace =\dfrac{9}{3}=3$ (答)
(2) $I=\displaystyle\int_{0}^{7}\dfrac{1}{\sqrt[3]{x+1}}\,dx$
解答
$I=\displaystyle\int_{0}^{7}(x+1)^{\scriptsize\dfrac{-1}{3}}\,dx=\dfrac{3}{2}\left\lbrack (x+1)^{\scriptsize\dfrac{2}{3}} \right\rbrack_{0}^{7}=\dfrac{3}{2}\left\lbrace 8^{\scriptsize\dfrac{2}{3}} -1^{\scriptsize\dfrac{2}{3}} \right \rbrace=\dfrac{3}{2}\left\lbrace (2^3)^{\scriptsize\dfrac{2}{3}} -1^{\scriptsize\dfrac{2}{3}} \right \rbrace$
$\quad =\dfrac{3}{2}(2^2-1)=\dfrac{9}{2}$ (答)
(3) $I=\displaystyle\int_{0}^{1}\dfrac{1}{x+1}\,dx$
解答
$I=\left\lbrack \mathrm{log}|x+1| \right\rbrack_{0}^{1}=\mathrm{log}2 -\underbrace{\mathrm{log}1}_{0} =\mathrm{log}2$ (答)
(4) $I=\displaystyle\int_{2}^{3}e^{2x-4}\,dx$
解答
$I=\dfrac{1}{2}\left\lbrack e^{2x-4} \right\rbrack_{2}^{3}=\dfrac{1}{2}\left(e^2 -\underbrace{e^0}_{1}\right) =\dfrac{e^2-1}{2}$ (答)
(5) $I=\displaystyle\int_{0}^{\scriptsize\dfrac{\pi}{4}}\mathrm{sin}3x\,dx$
解答
$I=\dfrac{-1}{3}\left\lbrack \mathrm{cos}3x \right\rbrack_{0}^{\scriptsize\dfrac{\pi}{4}}=\dfrac{-1}{3}\left(\mathrm{cos}\dfrac{3\pi}{4} -\underbrace{\mathrm{cos}0}_{1}\right) =\dfrac{-1}{3}\left(\dfrac{-\sqrt{2}}{2} -1\right) $
$\quad=\dfrac{1}{3}\cdot\dfrac{\sqrt{2}+2}{2}=\dfrac{\sqrt{2}+2}{6}$ (答)
(6) $I=\displaystyle\int_{0}^{\scriptsize\dfrac{\pi}{4}}\dfrac{1}{\mathrm{cos}^2x}\,dx$
解答
$I=\left\lbrack \mathrm{tan}x \right\rbrack_{0}^{\scriptsize\dfrac{\pi}{4}}=\underbrace{\mathrm{tan}\dfrac{\pi}{4}}_{1}-\underbrace{\mathrm{tan}0}_{0}=1$ (答)
(7) $I=\displaystyle\int_{0}^{3}\dfrac{1}{x^2+3}\,dx$
解答
$I=\dfrac{1}{\sqrt{3}}\left\lbrack \mathrm{Tan}^{-1}\dfrac{x}{\sqrt{3}} \right\rbrack_{0}^{3}=\dfrac{1}{\sqrt{3}}\left(\mathrm{Tan}^{-1}\dfrac{3}{\sqrt{3}} -\underbrace{\mathrm{Tan}^{-1}0}_{0}\right) $
$\quad =\dfrac{1}{\sqrt{3}}\mathrm{Tan}^{-1}\sqrt{3}=\dfrac{1}{\sqrt{3}}\cdot\dfrac{\pi}{3}=\dfrac{\sqrt{3}\pi}{9}$ (答)
(8) $I=\displaystyle\int_{0}^{\sqrt{2}}\dfrac{1}{\sqrt{4-x^2}}\,dx$
解答
$I=\left\lbrack \mathrm{Sin}^{-1}\dfrac{x}{2} \right\rbrack_{0}^{\sqrt{2}}=\mathrm{Sin}^{-1}\dfrac{\sqrt{2}}{2}-\underbrace{\mathrm{Sin}^{-1}0}_{0}=\dfrac{\pi}{4}$ (答)
行列の和・定数倍および積と逆行列
1.$A=\begin{pmatrix}3&-2\\1&-1\end{pmatrix},\;B=\begin{pmatrix}5&1\\-2&1\end{pmatrix}$ のとき次を求めよ。
(1) $2A-B$
解答
$2A-B=2\begin{pmatrix}3&-2\\1&-1\end{pmatrix}-\begin{pmatrix}5&1\\-2&1\end{pmatrix}=\begin{pmatrix}6&-4\\2&-2\end{pmatrix}-\begin{pmatrix}5&1\\-2&1\end{pmatrix}=\begin{pmatrix}1&-5\\4&-3\end{pmatrix}$ (答)
(2) $AB$
解答
$AB=\begin{pmatrix}3&-2\\1&-1\end{pmatrix} \begin{pmatrix}5&1\\-2&1\end{pmatrix}=\begin{pmatrix}3\cdot5+(-2)\cdot(-2)&3\cdot1+(-2)\cdot1\\1\cdot5+(-1)\cdot(-2)&1\cdot1+(-1)\cdot1\end{pmatrix}=\begin{pmatrix}19&1\\7&0\end{pmatrix}$ (答)
(3) $A^2$
解答
$A^2=\begin{pmatrix}3&-2\\1&-1\end{pmatrix}
\begin{pmatrix}3&-2\\1&-1\end{pmatrix}=\begin{pmatrix}3\cdot3+(-2)\cdot1 &3\cdot(-2)+(-2)\cdot(-1)\\1\cdot3+(-1)\cdot1 &1\cdot(-2)+(-1)\cdot(-1)\end{pmatrix}=\begin{pmatrix}7&-4\\2&-1\end{pmatrix}$ (答)
(4) $A^{-1}$
解答
$A^{-1}=\dfrac{1}{3\cdot(-1)-(-2)\cdot1}\begin{pmatrix}-1&-(-2)\\-1&3\end{pmatrix}=\dfrac{1}{-1}\begin{pmatrix}-1&2\\-1&3\end{pmatrix}=\begin{pmatrix}1&-2\\1&-3\end{pmatrix}$ (答)
2.次の行列の積を求めよ。
(1) $A=\begin{pmatrix}1&0&-1\\2&1&0\end{pmatrix} \begin{pmatrix}1&2\\0&-1\\1&1\end{pmatrix}$
解答
$A=\begin{pmatrix}1\cdot1+0\cdot0+(-1)\cdot1 & 1\cdot2+0\cdot(-1)+(-1)\cdot1
\\2\cdot1+1\cdot0+0\cdot1
& 2\cdot2+1\cdot(-1)+0\cdot1 \end{pmatrix}=\begin{pmatrix}0&1\\2&3\end{pmatrix}$ (答)
(2) $B=\begin{pmatrix}1&2\\0&-1\\1&1\end{pmatrix}\begin{pmatrix}1&0&-1\\2&1&0\end{pmatrix} $
解答
$B=\begin{pmatrix}1\cdot1+2\cdot2&1\cdot0+2\cdot1&1\cdot(-1)+2\cdot0\\0\cdot1+(-1)\cdot2&0\cdot0+(-1)\cdot1&0\cdot(-1)+(-1)\cdot0\\1\cdot1+1\cdot2&1\cdot0+1\cdot1&1\cdot(-1)+1\cdot0\end{pmatrix}=\begin{pmatrix}5&2&-1\\-2&-1&0\\3&1&-1\end{pmatrix}$ (答)
行列の冪乗とケーリー・ハミルトンの定理
3.$A=\begin{pmatrix}2&-6\\1&-2\end{pmatrix},\;B=\begin{pmatrix}3&1\\-4&-2\end{pmatrix}$ のとき次を求めよ。
(1) $A^5$
解答
公式 $A^2-(\mathrm{tr})A+|A|E=0$ (ケーレー・ハミルトンの定理) を用いる。
ただし、$E=\begin{pmatrix}1&0\\0&1\end{pmatrix}$ (単位行列)、$A=\begin{pmatrix}a&b\\c&d\end{pmatrix}$ のとき、$\mathrm{tr}A=a+d,\;|A|=ad-bc$
$\mathrm{tr}A=0,\;|A|=2$ よりケーリー・ハミルトンの定理から $A^2-0A+2E=0 \Rightarrow A^2=-2E$
よって $A^5=(A^2)^2A=(-2E)^2A=(-2)^2E^2A=4A=\begin{pmatrix}8&-24\\4&-8\end{pmatrix}$ (答)
(2) $B^6$
解答
行列 $A$ の固有方程式 $\varphi_A(\lambda)=\lambda^2-(\mathrm{tr}A)\lambda+|A|=0$ の解(固有値)が $\alpha\neq \beta$ のとき
公式 $A^n=\dfrac{\alpha^n-\beta^n}{\alpha-\beta}A+\dfrac{\alpha\beta^n-\beta\alpha^n}{\alpha-\beta}E$ ($E$ は単位行列) を用いる
$\mathrm{tr}A=1,\;|A|=-2$ より固有方程式は $\lambda^2-\lambda-2=(\lambda-2)(\lambda+1)=0$
よって、固有値は $\lambda=2, -1$ だから、
$B^6=\dfrac{2^6-(-1)^6}{2-(-1)}B+\dfrac{2\cdot(-1)^6-(-1)\cdot2^6}{2-(-1)}E=21B+22E$
$\quad=21\begin{pmatrix}5&1\\-2&1\end{pmatrix}+22\begin{pmatrix}1&0\\0&1\end{pmatrix}=\begin{pmatrix}85&21\\-84&-20\end{pmatrix}$ (答)
行列と連立方程式
4. $A=\begin{pmatrix}3&-2\\1&-1\end{pmatrix},\;B=\begin{pmatrix}5&1\\-2&1\end{pmatrix}$ のとき次をみたす行列 $C,\;D$ を求めよ。
(1) $AC=B$
解答
両辺に左から $A^{-1}=\dfrac{1}{-3-(-2)}\begin{pmatrix}-1&2\\-1&3\end{pmatrix}=\begin{pmatrix}1&-2\\1&-3\end{pmatrix}$ を掛けて、
$C=A^{-1}B=\begin{pmatrix}1&-2\\1&-3\end{pmatrix}\begin{pmatrix}5&1\\-2&1\end{pmatrix}=\begin{pmatrix}9&-1\\11&-2\end{pmatrix}$ (答)
(2) $DA=B$
解答
両辺に右から $A^{-1}=\dfrac{1}{-3-(-2)}\begin{pmatrix}-1&2\\-1&3\end{pmatrix}=\begin{pmatrix}1&-2\\1&-3\end{pmatrix}$ を掛けて、
$D=BA^{-1}=\begin{pmatrix}5&1\\-2&1\end{pmatrix}\begin{pmatrix}1&-2\\1&-3\end{pmatrix}=\begin{pmatrix}6&-13\\-1&1\end{pmatrix}$ (答)
5. 連立方程式 $\begin{cases}2x-3y = 3\\2x-5y = 1\end{cases}$ を行列表示して、(逆)行列を用いて解け。
解答
$\begin{pmatrix}2&-3\\2&-5\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}3\\1\end{pmatrix}$ より
$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}2&-3\\2&-5\end{pmatrix}^{-1}\begin{pmatrix}3\\1\end{pmatrix}=\dfrac{1}{2\cdot(-5)-(-3)\cdot2}\begin{pmatrix}-5&-(-3)\\-2&2\end{pmatrix}\begin{pmatrix}3\\1\end{pmatrix}$
$\hspace{24pt}=\dfrac{1}{-4}\begin{pmatrix}-12\\-4\end{pmatrix}=\begin{pmatrix}3\\1\end{pmatrix}$ よって $x=3, y=1$ (答)
定積分:三角関数の冪乗
1. 次の定積分の値を求めよ。
(1) $I=\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \left(\mathrm{sin}^4x+\mathrm{cos}^5x \right) \,dx$
解答
$\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{sin}^nx \,dx=\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{cos}^nx \,dx=\begin{cases}\dfrac{n-1}{n}\cdot\dfrac{n-3}{n-2}\cdots\dfrac{3}{4}\cdot\dfrac{1}{2}\cdot\dfrac{\pi}{2}\;(n:偶数)\\\dfrac{n-1}{n}\cdot\dfrac{n-3}{n-2}\cdots\dfrac{4}{5}\cdot\dfrac{2}{3}\cdot1\quad(n:奇数)\end{cases}$ を用いる
$I=\dfrac{3}{4}\cdot\dfrac{1}{2}\cdot\dfrac{\pi}{2}+\dfrac{4}{5}\cdot\dfrac{2}{3}\cdot1=\dfrac{3}{16}\pi+\dfrac{8}{15}$ (答)
(2) $I=\displaystyle \int_{0}^{\pi} \mathrm{sin}^6x \,dx$
解答
$\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{sin}^nx \,dx=\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{cos}^nx \,dx=\begin{cases}\dfrac{n-1}{n}\cdot\dfrac{n-3}{n-2}\cdots\dfrac{3}{4}\cdot\dfrac{1}{2}\cdot\dfrac{\pi}{2}\;(n:偶数)\\\dfrac{n-1}{n}\cdot\dfrac{n-3}{n-2}\cdots\dfrac{4}{5}\cdot\dfrac{2}{3}\cdot1\quad(n:奇数)\end{cases}$ を用いる
$I=2\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{sin}^6x \,dx=2\cdot\dfrac{5}{6}\cdot\dfrac{3}{4}\cdot\dfrac{1}{2}\cdot\dfrac{\pi}{2}=\dfrac{5}{16}\pi$ (答)
(3) $I=\displaystyle \int_{0}^{\pi} \mathrm{cos}^6x \,dx$
解答
$\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{sin}^nx \,dx=\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{cos}^nx \,dx=\begin{cases}\dfrac{n-1}{n}\cdot\dfrac{n-3}{n-2}\cdots\dfrac{3}{4}\cdot\dfrac{1}{2}\cdot\dfrac{\pi}{2}\;(n:偶数)\\\dfrac{n-1}{n}\cdot\dfrac{n-3}{n-2}\cdots\dfrac{4}{5}\cdot\dfrac{2}{3}\cdot1\quad(n:奇数)\end{cases}$ を用いる
$I=2\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{cos}^6x \,dx=2\cdot\dfrac{5}{6}\cdot\dfrac{3}{4}\cdot\dfrac{1}{2}\cdot\dfrac{\pi}{2}=\dfrac{5}{16}\pi$ (答)
(4) $I=\displaystyle \int_{0}^{\pi} \mathrm{cos}^7x \,dx$
解答
$J_1=\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{cos}^7x \,dx, J_2=\displaystyle \int_{\scriptsize\dfrac{\pi}{2}}^{\pi}$ とおくと、$y=\mathrm{cos}x$ のグラフの対称性より、
$7$(=奇数)乗であることに注意れば、$J_2=-J_1$ だから $I=J_1+J_2=J_1+(-J_1)=0$ (答)
定積分:部分積分
2.次の定積分の値を求めよ。
(1) $I=\displaystyle \int_{0}^{1} 4xe^{2x} \,dx$
解答
$I=\left\lbrack (2x-1)e^{2x}\right\rbrack _{0}^{1}=e^2-(-e^0)=e^2+1$(答)
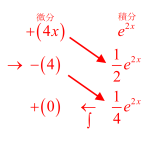
(2) $I=\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{10}} 25x\mathrm{sin}5x \,dx$
解答
$I=\left \lbrack -5x\mathrm{cos}5x+\mathrm{sin}5x \right\rbrack _{0}^{\scriptsize\dfrac{\pi}{10}}=\dfrac{-\pi}{2}\underbrace{\mathrm{cos}\dfrac{\pi}{2}}_{0}+\underbrace{\mathrm{sin}\dfrac{\pi}{2}}_{1}-\left( 0+\underbrace{\mathrm{sin}0}_{0} \right)=1$ (答)

(3) $I=\displaystyle \int_{1}^{e} x\mathrm{log}x \,dx$
解答
$I=\left \lbrack \dfrac{1}{2}x^2\mathrm{log}x-\dfrac{1}{2}\displaystyle \int x \,dx \right\rbrack _{0}^{e}=\left \lbrack \dfrac{1}{2}x^2\mathrm{log}x-\dfrac{1}{4}x^2 \right\rbrack _{0}^{e}$
$\quad=\underbrace{\dfrac{1}{2}e^2\underbrace{\mathrm{log}e}_{1}-\dfrac{1}{4}e^2}_{{\scriptsize\dfrac{1}{4}}e^2}-\left(\dfrac{1}{2}\underbrace{\mathrm{log}1}_{0}-\dfrac{1}{4}\right)=\dfrac{e^2+1}{4}$ (答)
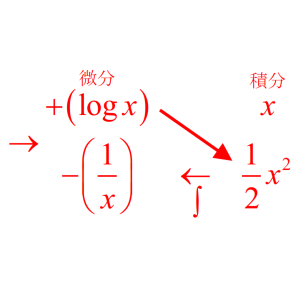
定積分:置換積分
3.次の定積分の値を求めよ。
(1) $I=\displaystyle \int_{0}^{3} \dfrac{x}{\sqrt{x+1}} \,dx$
解答
$t=\sqrt{x+1} \to t^2=x+1 \to \begin{array}{c} 2tdt=dx \\ x=t^2-1\end{array}\quad\begin{array}{c|cc} x & 0 & 3\\ \hline t & 1 & 2 \end{array}$ より
$I=\displaystyle \int_{1}^{2} \dfrac{t^2-1}{t} 2t\,dt=2\displaystyle \int_{1}^{2} (t^2-1) \,dt = 2\left\lbrack \dfrac{1}{3}t^3-t \right\rbrack_1^2 $
$\quad= 2 \left\lbrace \left(\dfrac{8}{3}-2\right)-\left(\dfrac{1}{3}-1\right) \right \rbrace =\dfrac{8}{3}$ (答)
(2) $I=\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} (\mathrm{sin}x+1)\mathrm{cos}x \,dx$
解答
$t=\mathrm{sin}x \to dt=\mathrm{cos}x\,dx \to \begin{array}{c|cc} x & 0 & \dfrac{\pi}{2}\\ \hline t=\mathrm{sin}x & 0 & 1 \end{array}$ より
$I=\displaystyle \int_{0}^{1} (t+1) \,dt = \left\lbrack \dfrac{1}{2}t^2+t \right\rbrack_0^1 = \dfrac{1}{2}+1=\dfrac{3}{2}$ (答)
(3) $I=\displaystyle \int_{0}^{1} \dfrac{2x+1}{x^2+x+1} \,dx$
解答
$t=x^2+x+1 \to dt=(2x+1)\,dx \to \begin{array}{c|cc} x & 0 & 1 \\ \hline t & 1 & 3 \end{array}$ より
$I=\displaystyle \int_{1}^{3} \dfrac{1}{t} \,dt = \left\lbrack \mathrm{log}|t| \right\rbrack_1^3 =\mathrm{log}|3|-\underbrace{\mathrm{log}|1|}_{0}=\mathrm{log}3$ (答)
(4) $I=\displaystyle \int_{1}^{e} \dfrac{\mathrm{log}x}{x} \,dx$
解答
$t=\mathrm{log}x \to dt=\dfrac{1}{x}\,dx \to \begin{array}{c|cc} x & 1 & e \\ \hline t=\mathrm{log}x & 0 & 1 \end{array}$ より
$I=\displaystyle \int_{0}^{1} t \,dt = \dfrac{1}{2}\left\lbrack t^2 \right\rbrack_0^1 =\dfrac{1}{2}\left(1^2-0^2\right)=\dfrac{1}{2}$ (答)
区分求積法と極限
1.次の極限値を求めよ。
(1) $I=\displaystyle \lim_{n\to\infty}\dfrac{1}{n^4}\left( 1^3+2^3+\cdots+(n-1)^3+n^3\right)$
解答
$I=\displaystyle \lim_{n\to\infty}\left( \left(\dfrac{1}{n}\right)^3+\cdots+\left(\dfrac{n-1}{n}\right)^3+\left(\dfrac{n}{n}\right)^3+\left(\dfrac{2}{n}\right)^3\right)\dfrac{1}{n}$
$\quad=\underbrace{\displaystyle \lim_{n\to\infty} \sum_k^n}_{\int_{0}^{1}} \quad \underbrace{\left( \dfrac{k}{n} \right)^3}_{x^3} \; \cdot \; \underbrace{\dfrac{1}{n}}_{dx}=\displaystyle \int_{0}^{1} x^3 \,dx=\dfrac{1}{4}\left\lbrack x^4 \right\rbrack_0^1=\dfrac{1}{4}(1-0)=\dfrac{1}{4}$ (答)
(2) $I=\displaystyle \lim_{n\to\infty}\left( \dfrac{n}{n^2+1^2}+\dfrac{n}{n^2+2^2}+\cdots+\dfrac{n}{n^2+(n-1)^2}+\dfrac{n}{n^2+n^2}\right)$
解答
$I=\displaystyle \lim_{n\to\infty}\left( \dfrac{1}{1+\left(\dfrac{1}{n}\right)^2}+\dfrac{1}{1+\left(\dfrac{1}{n}\right)^2}+\cdots+\dfrac{1}{1+\left(\dfrac{1}{n}\right)^2}+\dfrac{1}{1+\left(\dfrac{1}{n}\right)^2} \right)\dfrac{1}{n}$
$\quad=\underbrace{\displaystyle \lim_{n\to\infty} \sum_k^n}_{\int_{0}^{1}} \quad \underbrace{ \dfrac{1}{1+\left( \dfrac{k}{n} \right)^2}}_{\scriptsize\dfrac{1}{1+x^2}} \; \cdot \; \underbrace{\dfrac{1}{n}}_{dx}=\displaystyle \int_{0}^{1} \dfrac{1}{1+x^2} \,dx=\dfrac{1}{4}\left\lbrack \mathrm{Tan}^{-1}x \right\rbrack_0^1$
$\quad=\mathrm{Tan}^{-1}1-\underbrace{\mathrm{Tan}^{-1}0}_{0}=\dfrac{\pi}{4}$ (答)
面積
2.次の曲線や直線で囲まれた図形の面積 $S$ を求めよ。
(1) $y=\mathrm{cos}x\;\left(-\dfrac{\pi}{2}\leqq x \leqq \dfrac{\pi}{2}\right)$ と $x$ 軸
解答
$S=2\displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{cos}x \,dx=2\left\lbrack \mathrm{sin}x \right\rbrack_0^{\scriptsize\dfrac{\pi}{2}}=2\left( \underbrace{\mathrm{sin}\dfrac{\pi}{2}}_{1}- \underbrace{\mathrm{sin}0}_{0} \right)=2$ (答)
(2) $y=\sqrt{1-x}$ と $x$ 軸および $y$ 軸
解答
$x=1$ のとき $x$ 軸と交わるので
$S=\displaystyle \int_{0}^{1} \sqrt{1-x} \,dx=\displaystyle \int_{0}^{1} (1-x)^{\scriptsize\dfrac{1}{2}} \,dx=\dfrac{2}{-1\cdot3} \left\lbrack
(1-x)^{\scriptsize\dfrac{3}{2}} \right\rbrack_0^{1}=\dfrac{-2}{3}(0- 1)=\dfrac{2}{3}$ (答)
(3) 曲線 $y=x^2-2$ と 直線 $y=x$
解答
公式 $S=\displaystyle \int_{a}^{b} \left(\underbrace{y}_{上}-\underbrace{y}_{下}\right) \,dx$ を用いる
連立方程式 $\begin{cases}y=x^2-2\\y=x\end{cases}\;$ を解いて、交点の $x$ 座標は $x=-1, 2$ だから
$S=\displaystyle \int_{-1}^{2} \left\lbrace \underbrace{x}_{上}-\underbrace{\left(x^2-2\right)}_{下} \right\rbrace \,dx=\left\lbrack
\dfrac{x^2}{2}-\dfrac{x^3}{3}+2x \right\rbrack_{-1}^{2}$
$\quad=\left(2-\dfrac{8}{3}+4\right)-\left(\dfrac{1}{2}-\dfrac{-1}{3}-2\right)=\dfrac{9}{2}$ (答)
体積
3.次の曲線や直線で囲まれた図形を $x$ 軸の周りに回転してできる回転体の体積$V$ をめよ。
(1) $y=\mathrm{cos}x\;\left(-\dfrac{\pi}{2}\leqq x \leqq \dfrac{\pi}{2}\right)$ と $x$ 軸
解答
公式 $V=\pi\displaystyle \int_{a}^{b} y^2 \,dx$ を用いる
$V=2\cdot\pi \displaystyle \int_{0}^{\scriptsize\dfrac{\pi}{2}} \mathrm{cos}^2x \,dx=2\pi\cdot\dfrac{1}{2}\dfrac{\pi}{2}=\dfrac{\pi^2}{2}$ (答)
(2) $y=\sqrt{1-x}$ と $x$ 軸および $y$ 軸
解答
公式 $V=\pi\displaystyle \int_{a}^{b} y^2 \,dx$ を用いる
$S=\displaystyle \int_{0}^{1} \left(\sqrt{1-x}\right)^2 \,dx=\pi\displaystyle \int_{0}^{1} (1-x) \,dx=\pi \left\lbrack
x-\dfrac{x^2}{2} \right\rbrack_0^{1}=\dfrac{\pi}{2}$ (答)
曲線の長さ
4.曲線 $y=\dfrac{1}{8}x^4+\dfrac{1}{4x^4}\;\left(1\leqq x \leqq 2\right)$ の長さ $L$ をめよ。
解答
公式 $L=\displaystyle \int_{a}^{b} \sqrt{1+\left(y{\prime}\right)^2} \,dx$ を用いる
$1+\left(y{\prime}\right)^2=1+\left( \dfrac{x^3}{2}-\dfrac{1}{2x^2}\right)^2=1+\left(\dfrac{x^3}{2}\right)^3-\dfrac{1}{2}+\left( \dfrac{1}{2x^2}\right)$
$\quad=\left(\dfrac{x^3}{2}\right)^3+\dfrac{1}{2}+\left( \dfrac{1}{2x^2}\right)=\left( \dfrac{x^3}{2}+\dfrac{1}{2x^2}\right)^2$ より
$L=\displaystyle \int_{1}^{2} \sqrt{1+\left(y{\prime}\right)^2} \,dx=\pi\displaystyle \int_{1}^{2} \left(\dfrac{x^3}{2}+\dfrac{1}{2x^3}\right) \,dx= \left\lbrack
\dfrac{x^4}{8}-\dfrac{1}{4x^2} \right\rbrack_1^{2}$
$\quad=\left(\dfrac{16}{8}-\dfrac{1}{16}\right)-\left(\dfrac{1}{8}-\dfrac{1}{4}\right)=\dfrac{33}{16}$ (答)
広義積分
5.次の広義積分の値を求めよ。
(1) $I=\displaystyle \int_{0}^{1} \dfrac{1}{\sqrt{1-x^2}} \,dx$
解答
$I_{\epsilon}=\displaystyle \int_{0}^{1-\epsilon} \dfrac{1}{\sqrt{1-x^2}} \,dx=\left\lbrack
\mathrm{Sin}^{-1}x \right\rbrack_0^{1-\epsilon}=\mathrm{Sin}^{-1}(1-\epsilon)$ より
$I=\displaystyle \lim_{\epsilon \to +0} I_{\epsilon}=\displaystyle \lim_{\epsilon \to +0} \mathrm{Sin}^{-1}(1-\epsilon)=\mathrm{Sin}^{-1}1=\dfrac{\pi}{2}$ (答)
(2) $I=\displaystyle \int_{1}^{\infty} \dfrac{1}{x^2} \,dx$
解答
$I_M=\displaystyle \int_{1}^{M} \dfrac{1}{x^2} \,dx=\left\lbrack
\dfrac{1}{-x} \right\rbrack_0^{M}=\dfrac{1}{-M}-\dfrac{1}{-1}$ より
$I=\displaystyle \lim_{M \to \infty} I_{M}=\displaystyle \lim_{M \to \infty} \left(\dfrac{-1}{M} +1 \right)=0+1=1$ (答)
(3) $I=\displaystyle \int_{\sqrt{3}}^{\infty} \dfrac{1}{x^2+1} \,dx$
解答
$I_M=\displaystyle \int_{\sqrt{3}}^{M} \dfrac{1}{x^2+1} \,dx=\left\lbrack
\mathrm{Tan}^{-1}x \right\rbrack_1^{M}=\mathrm{Tan}^{-1}M-\mathrm{Tan}^{-1}\sqrt{3}$ より
$I=\displaystyle \lim_{M \to \infty} I_{M}=\displaystyle \lim_{M \to \infty} \left(\mathrm{Tan}^{-1}M-\mathrm{Tan}^{-1}\sqrt{3} \right)=\underbrace{\mathrm{Tan}^{-1}\infty}_{\scriptsize\dfrac{\pi}{2}}-\underbrace{\mathrm{Tan}^{-1}\sqrt{3}}_{\scriptsize\dfrac{\pi}{3}}=\dfrac{\pi}{6}$ (答)
対称変換
1. 次の対称変換を表す行列を求めよ。
(1) $x$ 軸対称変換
解答
$\begin{cases}x^{\prime}=x+0\cdot y\\y^{\prime}=0\cdot x-y\end{cases}\;\Rightarrow\;\begin{pmatrix}1&0\\0&-1\end{pmatrix}$ (答)
(2) $y$ 軸対称変換
解答
$\begin{cases}x^{\prime}=-x+0\cdot y\\y^{\prime}=0\cdot x+y\end{cases}\;\Rightarrow\;\begin{pmatrix}-1&0\\0&1\end{pmatrix}$ (答)
(3) 原点対称変換
解答
$\begin{cases}x^{\prime}=-x+0\cdot y\\y^{\prime}=0\cdot x-y\end{cases}\;\Rightarrow\;\begin{pmatrix}-1&0\\0&-1\end{pmatrix}$ (答)
(4) 直線 $y=x$ に関する対称変換
解答
$\begin{cases}x^{\prime}=0\cdot x+y\\y^{\prime}=x+0\cdot y\end{cases}\;\Rightarrow\;\begin{pmatrix}0&1\\1&0\end{pmatrix}$ (答)
1次変換の像と原像(=逆像)
2. 一次変換 $\begin{cases}x^{\prime}=2x+3y\\y^{\prime}=x+2y\end{cases}$ について、次を求めよ。
(1) 点 $\mathrm{P}(1, 2)$ の像 $\mathrm{P}^{\prime}$
解答
$\begin{pmatrix}2&3\\1&2\end{pmatrix}\begin{pmatrix}1\\2\end{pmatrix}=\begin{pmatrix}8\\5\end{pmatrix}\;\Rightarrow\;\mathrm{P}^{\prime}(8, 5)$ (答)
(2) 点 $\mathrm{Q}^{\prime}(3, 1)$ の原像(=逆像) $\mathrm{Q}(x, y)$
解答
公式 $\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}=\dfrac{1}{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}$ を用いる
$\begin{pmatrix}2&3\\1&2\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}3\\1\end{pmatrix}\;\Rightarrow\;\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}2&3\\1&2\end{pmatrix}^{-1}\begin{pmatrix}3\\1\end{pmatrix}=\dfrac{1}{4-3}\begin{pmatrix}2&-3\\-1&2\end{pmatrix}\begin{pmatrix}3\\1\end{pmatrix}=\begin{pmatrix}3\\-1\end{pmatrix}$
$\mathrm{Q}(3, -1)$ (答)
原点周りの回転
3. 点 ${\mathrm{P}}(\sqrt{3}, 1)$ を原点の周りに$120^{\circ}$ 回転した点 $\mathrm{P}^{\prime}$ を求めよ。
解答
(原点周りの $\theta$ 回転の行列) $\begin{pmatrix}\mathrm{cos}\theta&-\mathrm{sin}\theta\\\mathrm{sin}\theta&\mathrm{cos}\theta\end{pmatrix}$ を用いる
$\begin{pmatrix}\mathrm{cos}120^{\circ}&-\mathrm{sin}120^{\circ}\\\mathrm{sin}120^{\circ}&\mathrm{cos}120^{\circ}\end{pmatrix}\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}=\dfrac{1}{2}\begin{pmatrix}-1 & -\sqrt{3} \\ \sqrt{3} & -1\end{pmatrix}\begin{pmatrix}\sqrt{3} \\ 1\end{pmatrix}=\dfrac{1}{2}\begin{pmatrix}-2\sqrt{3}\\ 2\end{pmatrix}=\begin{pmatrix}-\sqrt{3}\\1\end{pmatrix}$
$\mathrm{P}^{\prime}(-\sqrt{3}, 1)$ (答)
1次変換の合成と逆変換
4.一次変換 $f:\begin{cases}x^{\prime}=2x+3y\\y^{\prime}=x+2y\end{cases},g:\begin{cases}x^{\prime}=x-2y\\y^{\prime}=x+3y\end{cases}\;$ について、次の問いに答えよ。
(1) $f$ の逆変換 $f^{-1}$ を表す行列を求めよ。
解答
公式 $\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}=\dfrac{1}{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}$ を用いる
$\underbrace{\begin{pmatrix}2&3\\1&2\end{pmatrix}^{-1}}_{f^{-1}}=\dfrac{1}{4-3}\begin{pmatrix}2&-3\\-1&2\end{pmatrix}=\begin{pmatrix}2&-3\\-1&2\end{pmatrix}$ (答)
(2) 合成 $f^{-1}\circ g$ を表す行列を求めよ。
解答
$\underbrace{\begin{pmatrix}2&-3\\-1&2\end{pmatrix}}_{f^{-1}}\;\underbrace{\begin{pmatrix}1&-2\\1&3\end{pmatrix}}_{g}=\begin{pmatrix}-1&-13\\1&8\end{pmatrix}$ (答)
1次変換による直線の像
5.次の1次変換による直線 $y=2x+1$ の像を求めよ。
(1) $f:\begin{cases}x^{\prime}=-2x+2y\\y^{\prime}=x+y\end{cases}$
解答
$\begin{cases}x^{\prime}=-2x+2(2x+1)=2x+2\\y^{\prime}=x+(2x+1)=3x+1\end{cases}\;\Rightarrow\;\underbrace{3x^{\prime}}_{6x+6}-\underbrace{2y^{\prime}}_{-6x+2}=4\;\Rightarrow\;2y^{\prime}=3x^{\prime}-4$ より
直線 $y=\dfrac{3}{2}x-2$ (答)
(2) $g:\begin{cases}x^{\prime}=3x+6y\\y^{\prime}=x+2y\end{cases}$
解答
$\begin{cases}x^{\prime}=3x+6(2x+1)=15x+6\\y^{\prime}=x+2(2x+1)=5x+2\end{cases}\;\Rightarrow\;\underbrace{y^{\prime}}_{5x+2}=\dfrac{1}{3}\underbrace{x^{\prime}}_{15x+6}$ より、直線 $y=\dfrac{1}{3}x$ (答)
(3) $h:\begin{cases}x^{\prime}=2x-y\\y^{\prime}=-4x+2y\end{cases}$
解答
$\begin{cases}x^{\prime}=2x-(2x+1)=-1\\y^{\prime}=-4x+2(2x+1)=2\end{cases}\;$ より、1点 $(-1, 2)$ (答)
1次変換の決定問題
6. 1次変換 $f$ による点 $\mathrm{P}(2, 1),\;\mathrm{Q}(1, 1)$ の像が $\mathrm{P}^{\prime}(-1, 3),\;\mathrm{Q}^{\prime}(0, 2)$ のとき、$f$ を表す行列 $A$ を求めよ。
解答
公式 $\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}=\dfrac{1}{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}$ より $\begin{pmatrix}2&1\\1&1\end{pmatrix}^{-1}=\dfrac{1}{2-1}\begin{pmatrix}1&-1\\-1&2\end{pmatrix}$ に注意する
$A\begin{pmatrix}2&1\\1&1\end{pmatrix}=\begin{pmatrix}-1&0\\3&2\end{pmatrix}$
$\Rightarrow\;A=\begin{pmatrix}-1&0\\3&2\end{pmatrix}\begin{pmatrix}2&1\\1&1\end{pmatrix}^{-1}=\begin{pmatrix}-1&0\\3&2\end{pmatrix}\begin{pmatrix}1&-1\\-1&2\end{pmatrix}=\begin{pmatrix}-1&1\\1&1\end{pmatrix}$(答)
行列の正則条件
7.行列 $A=\begin{pmatrix}2&x\\3&6\end{pmatrix}$ が正則でないとき、$x$ を求めよ。
解答
$|A|=\mathrm{det}A=\begin{array}{|cc|}2&x\\3&6\end{array}=\mathrm{det}\begin{pmatrix}2&x\\3&6\end{pmatrix}=12-3x=0\;\Rightarrow\;x=4$ (答)
行列式と面積
8. $x^2+y^2=1$ の1次変換 $f:\begin{cases}x^{\prime}=2x \\ y^{\prime}=3y\end{cases} $ による像を求め、像が囲む面積も求めよ。
解答
公式 $\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}=\dfrac{1}{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}$ より
$\begin{pmatrix}2&0\\0&3\end{pmatrix}^{-1}=\dfrac{1}{6-0}\begin{pmatrix}3&0\\0&2\end{pmatrix}=\begin{pmatrix}\dfrac{1}{2}&0\\0&\dfrac{1}{3}\end{pmatrix}$ に注意する
$\begin{pmatrix}2&0\\0&3\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}x^{\prime}\\y^{\prime}\end{pmatrix}\;\Rightarrow\;\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}2&0\\0&3\end{pmatrix}^{-1}\begin{pmatrix}x^{\prime}\\y^{\prime}\end{pmatrix}=\begin{pmatrix}\dfrac{1}{2}&0\\0&\dfrac{1}{3}\end{pmatrix}\begin{pmatrix}x^{\prime}\\y^{\prime}\end{pmatrix}=\begin{pmatrix}\dfrac{x^{\prime}}{2}\\ \dfrac{y^{\prime}}{3}\end{pmatrix}$ より
像は $\;\underbrace{\left(
\dfrac{x^{\prime}}{2} \right)^{2}}_{x^2}+\underbrace{\left( \dfrac{y^{\prime}}{3} \right)^{2}}_{y^2}=1\;\Rightarrow\;$ 楕円 $\;\dfrac{x^2}{4}+\dfrac{y^2}{9}=1$ (答)
面積は $\underbrace{(\text{半径1の円の面積})}_{\pi}\times\underbrace{\left|\mathrm{det}\begin{pmatrix}2&0\\0&3\end{pmatrix}\right|}_{6}=6\pi$ (答)