関数の微分I
1. 次の関数を微分せよ。
(1) $y=3x^2-5x+4$
解答
公式 $(c)’=0$ 、$(x)’=1$、$(x^n)’=nx^{n-1}$および微分の線形性を用いる
$y’=6x-5$ (答)
(2) $y=\dfrac{1}{3x^6}$
解答
$y=\dfrac{1}{3}\cdot\dfrac{1}{x^6}$ に注意して、公式 $\dfrac{1}{x^n}=\dfrac{-n}{x^{n+1}}$ を用いる
$y’=\dfrac{1}{3}\cdot\dfrac{-6}{x^7}=\dfrac{-2}{x^7}$ (答)
(3) $y=\sqrt[3]{x^4}$
解答
$y=x^{\scriptsize\dfrac{4}{3}}$ に注意して、公式 $(x^a)=ax^{a-1}$ を用いる
$y’=\dfrac{4}{3}x^{\scriptsize\dfrac{1}{3}}=\dfrac{4}{3}\sqrt[3]{x}$ (答)
(4) $y=\dfrac{1}{\sqrt[6]{x}}$
解答
$y=x^{\scriptsize\dfrac{-1}{6}}$ に注意して、公式 $(x^a)=ax^{a-1}$ を用いる
$y’=\dfrac{-1}{6}x^{\scriptsize{\dfrac{-7}{6}}}=\dfrac{-1}{6\sqrt[6]{x^7}}=\dfrac{-1}{6x\sqrt[6]{x}}$(答)
(5) $y=(x^2-3x+5)^3$
解答
公式 $(f^n)’=n\cdot f’\cdot f^{n-1}$ を用いる
$y’=3(x^2-3x+5)'(x^2-3x+5)^2=3(2x-3)(x^2-3x+5)^2$ (答)
(6) $y=\dfrac{1}{(4x-7)^6}$
解答
公式 $\left( \dfrac{1}{f^n} \right)^{\prime}= \dfrac{-nf’}{f^{n+1}}$ を用いる
$y’=\dfrac{-6\cdot(4x-7)’}{(4x-7)^7}=\dfrac{-6\cdot4}{(4x-7)^7}=\dfrac{-24}{(4x-7)^7}$ (答)
(7) $y=\sqrt[3]{3x+5}$
解答
$y=(3x+5)^{\scriptsize\dfrac{1}{3}}$ に注意して、公式 $(f^a)’=a\cdot f’\cdot f^{a-1}$ を用いる
$y’=\dfrac{1}{3}(3x+5)'(3x+5)^{\scriptsize{-\dfrac{2}{3}}}=\dfrac{1}{3}\cdot 3 \dfrac{1}{\sqrt[3]{(3x+5)^2}}=\dfrac{1}{\sqrt[3]{(3x+5)^2}}$ (答)
(8) $y=\sqrt{1-x^2}$
解答
公式 $(\sqrt{f})’=\dfrac{f’}{2\sqrt{f}}$ を用いる
$y’=\dfrac{(1-x^2)’}{2\sqrt{1-x^2}}=\dfrac{-2x}{2\sqrt{1-x^2}}=\dfrac{-x}{\sqrt{1-x^2}}$ (答)
(9) $y=\dfrac{3x-1}{x^2+1}$
解答
公式 $\left( \dfrac{f}{g} \right)^{\prime}=\dfrac{f’g-fg’}{g^2}$ を用いる
$(分子)=(3x-1)'(x^2+1)-(3x-1)(x^2+1)’=3(x^2+1)-2x(3x-1)=-3x^2+2x+3$
$y’=\dfrac{-3x^2+2x+3}{(x^2+1)^2}$ (答)
(10) $y=(2x+1)^4(3x-1)^5$
解答
公式 $(f^ng^m)’=(nf’g+mfg’)f^{n-1}g^{m-1}$ を用いる
$4(2x+1)'(3x-1)+5(2x+1)(3x-1)’=4\cdot 2(3x-1)+5\cdot3(2x+1)=54x+7$
$y’=(54x+7)(2x+1)^3(3x-1)^4$ (答)
(11) $y=\dfrac{(2x+1)^6}{(3x-1)^3}$
解答
公式 $\left(\dfrac{f^n}{g^m}\right)^{\prime}=\dfrac{(nf’g-mfg’)f^{n-1}}{g^{m+1}}$ を用いる
$6(2x+1)'(3x-1)-3(2x+1)(3x-1)’=6\cdot 2(3x-1)-3\cdot3(2x+1)=18x-21$
$y’=\dfrac{(18x-21)(2x+1)^5}{(3x-1)^4}=\dfrac{3(6x-7)(2x+1)^5}{(3x-1)^4}$ (答)
(12) $y=x^x\;(x>0)$
解答
対数微分の公式 $y’=y({\mathrm{log}}y)’$ を用いる
$({\mathrm{log}}y)’=({\mathrm{log}}x^x)’=(x{\mathrm{log}}x)’=(x)'{\mathrm{log}}x+x({\mathrm{log}}x)’=1\cdot{\mathrm{log}}x+x\cdot \dfrac{1}{x}=1+{\mathrm{log}}x$
$y’=x^x(1+{\mathrm{log}}x)$ (答)
関数の微分II
1. 次の関数を微分せよ。
(1) $y={\mathrm{log}}(x^2+x-1)$
解答
公式 $({\mathrm{log}}f)’=({\mathrm{log}}|f|)’=\dfrac{f’}{f}$を用いる
$y’=\dfrac{(x^2+x-1)’}{x^2+x-1}=\dfrac{2x+1}{x^2+x-1}$ (答)
(2) $y={\mathrm{log}}|4x-3|$
解答
公式 $({\mathrm{log}}f)’=({\mathrm{log}}|f|)’=\dfrac{f’}{f}$ を用いる
$y’=\dfrac{(4x-3)’}{4x-3}=\dfrac{4}{4x-3}$ (答)
(3) $y={\mathrm{log}}_3|7x+4|$
解答
公式 $({\mathrm{log}}_af)’=({\mathrm{log}}_a|f|)’=\dfrac{f’}{f{\mathrm{log}}a}$ を用いる
$y’=\dfrac{(7x+4)’}{(7x+4){\mathrm{log}}3}=\dfrac{7}{(7x+4){\mathrm{log}}3}$ (答)
(4) $y=3^{2x+1}$
解答
公式 $(a^f)’=f’a^f{\mathrm{log}}a$ を用いる
$y’=(2x+1)’3^{2x+1}{\mathrm{log}}3=2\cdot3^{2x+1}{\mathrm{log}}3$ (答)
(5) $y=e^{x^2-3x-2}$
解答
公式 $(e^f)’=f’e^f$ を用いる
$y’=(x^2-3x-2)’e^{x^2-3x-2}=(2x-3)e^{x^2-3x-2}$ (答)
(6) $y=x{\mathrm{sin}}x$
解答
公式 $(fg)’=f’g+fg’$ および $({\mathrm{sin}}x)’={\mathrm{cos}}x$ を用いる
$y’=(x)'{\mathrm{sin}}x+x({\mathrm{sin}}x)’={\mathrm{sin}}x+x{\mathrm{cos}}x$ (答)
(7) $y=\dfrac{{\mathrm{sin}}x}{1+{\mathrm{cos}}x}$
解答
公式 $\left(\dfrac{f}{g}\right)^{\prime}=\dfrac{f’g-fg’}{g^2}$ 、$({\mathrm{sin}}x)’={\mathrm{cos}}x$ および $({\mathrm{cos}}x)’=-{\mathrm{sin}}x$ を用いる
(分子)$=({\mathrm{sin}}x)'(1+{\mathrm{cos}}x)-{\mathrm{sin}}x(1+{\mathrm{cos}}x)’={\mathrm{cos}}x(1+{\mathrm{cos}}x)-(-{\mathrm{sin}}x)$
$\quad \quad \;={\mathrm{cos}}x+{\mathrm{cos}}^2x+{\mathrm{sin}}^2x={\mathrm{cos}}x+1$ $({\mathrm{cos}}^2x+{\mathrm{sin}}^2x=1)$ に注意する
$y’=\dfrac{1+{\mathrm{cos}}x}{(1+{\mathrm{cos}}x)^2}=\dfrac{1}{1+{\mathrm{cos}}x}$ (答)
(8) $y={\mathrm{tan}}(2x+1)$
解答
公式 $({\mathrm{tan}}f)’=\dfrac{f’}{{\mathrm{cos}}^2f}$ を用いる
$y’=\dfrac{(2x+1)’}{{\mathrm{cos}}^2(2x+1)}=\dfrac{2}{{\mathrm{cos}}^2(2x+1)}$ (答)
(9) $y={\mathrm{Sin}}^{-1}3x$
解答
$({\mathrm{Sin}}^{-1}x)’=\dfrac{1}{\sqrt{1-x^2}}、 ({\mathrm{Sin}}^{-1}f)’=\dfrac{f’}{\sqrt{1-f^2}}、 \left({\mathrm{Sin}}^{-1}\dfrac{x}{a}\right)^{\prime}=\dfrac{1}{\sqrt{a^2-x^2}}$ に注意する
$y’=\dfrac{(3x)’}{\sqrt{1-(3x)^2}}=\dfrac{3}{\sqrt{1-9x^2}}$ (答)
(10) $y={\mathrm{Tan}}^{-1}\dfrac{x}{3}$
解答
$({\mathrm{Tan}}^{-1}x)’=\dfrac{1}{x^2+1}、({\mathrm{Tan}}^{-1}f)’=\dfrac{f’}{f^2+1}、\left({\mathrm{Tan}}^{-1}\dfrac{x}{a}\right)^{\prime}=\dfrac{a}{x^2+a^2}$ に注意する
$y’=\dfrac{3}{x^2+3^2}=\dfrac{3}{x^2+9}$ (答)
(11) $y=e^{2x}{\mathrm{sin}}3x$
解答
公式 $(fg)’=f’g+fg’$、$(e^f)’=f’e^f$、$({\mathrm{sin}}f)’=f'{\mathrm{cos}}f$ を用いる
$y’=(e^{2x})'({\mathrm{sin}}3x)+(e^{2x})({\mathrm{sin}}3x)’=2e^{2x}{\mathrm{sin}}3x+e^{2x}(3{\mathrm{cos}}3x)=e^{2x}(2{\mathrm{sin}}3x+3{\mathrm{cos}}3x)$ (答)
(12) $y={\mathrm{cos}}^{5}2x$
解答
公式 $(f^n)’=nf’f^{n-1}$、$({\mathrm{cos}}f)’=-f'{\mathrm{sin}}f$ を用いる
$y={\mathrm{cos}}^{5}2x=({\mathrm{cos}}2x)^5$ に注意する
$y’=5({\mathrm{cos}}2x)'({\mathrm{cos}}2x)^4=5(-2{\mathrm{sin}}2x)({\mathrm{cos}}2x)^4=-10{\mathrm{sin}}2x{\mathrm{cos}}^42x$ (答)
ベクトルの線形和
1. 下図のベクトル $\vec{c}$、$\vec{d}$ をベクトル $\vec{a}$、$\vec{b}$ を用いて表せ
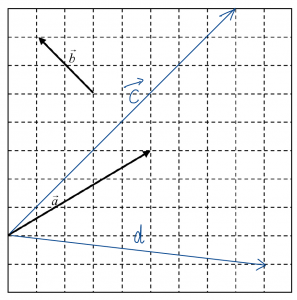
解答
$\vec{c}=2\vec{a}+\vec{b}$、$\vec{d}=\vec{a}-2\vec{b}$ (答) (下図参照)
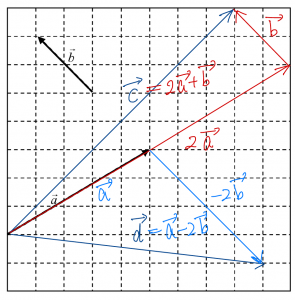
交点の位置ベクトル
2. $\triangle {\mathrm{ABC}}$ において、$\overrightarrow{\mathrm{OA}}=\vec{a}$、$\overrightarrow{\mathrm{OB}}=\vec{b}$ とし、点${\mathrm{C}}$は線分${\mathrm{OA}}$を1:2に内分する点、点${\mathrm{D}}$は線分${\mathrm{OB}}$を2:1に内分する点とする 線分${\mathrm{BC}}$と線分${\mathrm{AD}}$の交点を${\mathrm{P}}$とするとき、ベクトル$\overrightarrow{\mathrm{OP}}$を$\vec{a}$、$\vec{b}$で表せ
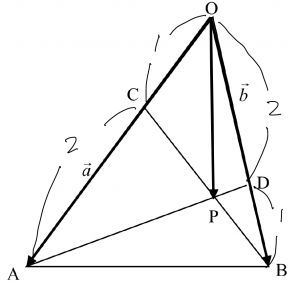
解答
(公式) 直線${\mathrm{AB}}$の$t$を媒介変数とするベクトル方程式 $\;\vec{p}=\overrightarrow{\mathrm{OP}}=(1-t)\vec{a}+t\vec{b}$ を用いる
$\vec{c}=\overrightarrow{\mathrm{OC}}=\dfrac{1}{3}\vec{a}$、$\vec{d}=\overrightarrow{\mathrm{OD}}=\dfrac{2}{3}\vec{b}$ より
直線${\mathrm{CB}}:\vec{p}=(1-t)\vec{c}+t\vec{b}=\dfrac{1-t}{3}\vec{a}+t\vec{b}$、直線${\mathrm{AD}}:\vec{p}=(1-s)\vec{a}+s\vec{d}=(1-s)\vec{a}+\dfrac{2s}{3}\vec{b}$
だから$\;\begin{cases}\dfrac{1-t}{3}=1-s\\t=\dfrac{2s}{3}\end{cases} \Rightarrow \begin{cases}t+3s=1\\3t+2s=2\end{cases} \Rightarrow \begin{cases}t=\dfrac{4}{7}\\s=\dfrac{1}{7}\end{cases}$ よって $\vec{p}=\dfrac{1}{7}\vec{a}+\dfrac{4}{7}\vec{b}$ (答)
(別解1:メネラウスの定理を用いる)
$\overrightarrow{\mathrm{CP}}=t\overrightarrow{\mathrm{CB}}$ とおくと $\vec{p}=\vec{c}+t\overrightarrow{\mathrm{CB}}=\vec{c}+t(\vec{b}-\vec{c})=(1-t)\vec{c}+t\vec{b}$
ここで、メネラウスの定理より $\dfrac{3}{2}\cdot\dfrac{t}{1-t}\cdot\dfrac{1}{2}=1 \Rightarrow 3t=4(1-t) \Rightarrow t=\dfrac{4}{7}$
よって $\vec{p}=\dfrac{3}{7}\vec{c}+\dfrac{4}{7}\vec{b}$ ここで、$\vec{c}=\dfrac{1}{3}\vec{a}$ より$\vec{p}=\dfrac{1}{3}\cdot\dfrac{3}{7}\vec{a}+\dfrac{4}{7}\vec{b}=\dfrac{1}{7}\vec{a}+\dfrac{4}{7}\vec{b}$ (答)
(別解2:簡易公式を用いる)
一般に、${\mathrm{OA}}$ を $a_1:a_2$ に内分する点を ${\mathrm{C}}$、${\mathrm{OB}}$ を $b_1:b_2$ に内分する点を ${\mathrm{D}}$ とすると $\alpha=a_1b_2, \beta=b_1a_2, \gamma=a_2b_2 \Rightarrow \vec{p}=\dfrac{\alpha}{\alpha+\beta+\gamma}\vec{a}+\dfrac{\beta}{\alpha+\beta+\gamma}\vec{b}\;$ (簡易公式)$\quad$が成り立つ
$\alpha=1\cdot, \beta=2\cdot 2=4, \gamma=2\cdot 1=2$ より $\vec{p}=\dfrac{1}{1+4+2}\vec{a}+\dfrac{4}{1+4+2}\vec{b}=\dfrac{1}{7}\vec{a}+\dfrac{4}{7}\vec{b}$ (答)
ベクトルの成分表示
3. $\vec{a}=\begin{pmatrix}1\\-2\end{pmatrix}$、$\vec{b}=\begin{pmatrix}2\\1\end{pmatrix}$、$\vec{c}=\begin{pmatrix}-1\\3\end{pmatrix}$ とするとき、次を求めよ
(1) $2\vec{a}-\vec{b}+3\vec{c}\quad$ (2) $|\vec{b}-\vec{a}|\quad$ (3) $\vec{a}\cdot(\vec{b}-2\vec{c})$
解答
(公式) $\vec{a}=\begin{pmatrix}a_1\\a_2\end{pmatrix}$、$\vec{b}=\begin{pmatrix}b_1\\b_2\end{pmatrix}$ のとき、$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2$、 $|\vec{a}|=a_1^2+a_2^2$ を用いる
(1) $2\begin{pmatrix}1\\-2\end{pmatrix}-\begin{pmatrix}2\\1\end{pmatrix}+3\begin{pmatrix}-1\\3\end{pmatrix}=\begin{pmatrix}2\cdot 1-2+3\cdot(-1)\\2\cdot(-2)-1+3\cdot3\end{pmatrix}=\begin{pmatrix}-3\\4\end{pmatrix}\quad$ (答)
(2) $\left |\begin{pmatrix}2\\1\end{pmatrix}-\begin{pmatrix}1\\-2\end{pmatrix}\right |=\left |\begin{pmatrix}1\\3\end{pmatrix}\right |=\sqrt{1^2+3^2}=\sqrt{10}\quad$ (答)
(3) $\begin{pmatrix}1\\-2\end{pmatrix}\cdot \left \lbrace\begin{pmatrix}2\\1\end{pmatrix}-2\begin{pmatrix}-1\\3\end{pmatrix} \right \rbrace =\begin{pmatrix}1\\-2\end{pmatrix}\cdot\begin{pmatrix}4\\-5\end{pmatrix}=1\cdot 4 +(-2)\cdot(-5)=14\quad$ (答)
ベクトルの内積
4. 次の問いに答えよ
(1) $|\vec{a}|=2$、$|\vec{b}|=3$、$\theta=\dfrac{2\pi}{3}$ のとき内積 $\vec{a}\cdot\vec{b}$ を求めよ ($\theta$ はベクトル $\vec{a}$ と $\vec{b}$ のなす角)
解答
$\begin{matrix} \theta & 0^{\circ} & 30^{\circ} & 45^{\circ} & 60^{\circ} & 90^{\circ} & 120^{\circ} & 135^{\circ} & 150^{\circ} & 180^{\circ} \\ {\mathrm{cos}}\theta & 1& \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0 & \dfrac{-1}{2} & \dfrac{-\sqrt{2}}{2} & \dfrac{-\sqrt{3}}{2} & -1 \end{matrix}$
(定義) $\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|{\mathrm{cos}}\theta$ を用いる
$\vec{a}\cdot\vec{b}=2\cdot3{\mathrm{cos}}\dfrac{2\pi}{3}=6{\mathrm{cos}}120^{\circ}=6\cdot\dfrac{-1}{2}=-3$ (答)
(2) $\vec{a}=\begin{pmatrix}2\sqrt{3}\\1\end{pmatrix}$、$\vec{b}=\begin{pmatrix}-7\\\sqrt{3}\end{pmatrix}$ のとき、$\vec{a}$ と $\vec{b}$ のなす角 $\theta$ を求めよ
解答
$\begin{matrix}\theta & 0^{\circ} & 30^{\circ} & 45^{\circ} & 60^{\circ} & 90^{\circ} & 120^{\circ} & 135^{\circ} & 150^{\circ} & 180^{\circ} \\ {\mathrm{cos}}\theta & 1& \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0 & \dfrac{-1}{2} & \dfrac{-\sqrt{2}}{2} & \dfrac{-\sqrt{3}}{2} & -1 \end{matrix}$
(公式) ${\mathrm{cos}}\theta=\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}$ より $\theta={\mathrm{Cos}}^{-1}\left(\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\right)$ を用いる
$\vec{a}\cdot\vec{b}=-14\sqrt{3}+\sqrt{3}=-13\sqrt{3}$、$|\vec{a}|=\sqrt{12+1}=\sqrt{13}$、$|\vec{b}|=\sqrt{49+3}=\sqrt{52}=2\sqrt{13}$
よって、$\theta={\mathrm{Cos}}^{-1}\left( \dfrac{-13\sqrt{3}}{\sqrt{13}\cdot 2\sqrt{13}} \right)={\mathrm{Cos}}^{-1}\left(\dfrac{-\sqrt{3}}{2}\right)=120^{\circ}=\dfrac{5\pi}{6}$ (答)
(3) $|\vec{a}|=3$、$|\vec{b}|=2$、$|2\vec{a}-3\vec{b}|=6$ のとき、内積 $\vec{a}\cdot\vec{b}$ を求めよ
解答
(公式) $|\vec{a}|^2=\vec{a}\cdot\vec{a}$ を用いる
$|2\vec{a}-3\vec{b}|^2=4|\vec{a}|^2-12\vec{a}\cdot\vec{b}+9|\vec{b}|^2$ より $\vec{a}\cdot\vec{b}=\dfrac{4|\vec{a}|^2+9|\vec{b}|^2-|2\vec{a}-3\vec{b}|^2}{12}=\dfrac{4\cdot3^2+9\cdot2^2-6^2}{12}=3$ (答)
(4) $|\vec{a}|=4$、$|\vec{b}|=3$、$\vec{a}\cdot\vec{b}=-6$ のとき $|\vec{a}-2\vec{b}|$ を求めよ
解答
(公式) $|\vec{a}|^2=\vec{a}\cdot\vec{a}$ を用いる
$|\vec{a}-2\vec{b}|^2=|\vec{a}|^2-4\vec{a}\cdot\vec{b}+4|\vec{b}|^2=4^2-4\cdot(-6)+4\cdot3^2=76$ より $|\vec{a}-2\vec{b}|=\sqrt{76}=2\sqrt{19}$ (答)
接線の方程式
1. 次の曲線の( )内の $x$ の値に対応する点における接線の方程式を求めよ
(1) $y=\sqrt{x}\quad(x=1)$
解答
($x=a$に対応する点における接線の公式)$y=f'(a)(x-a)+f(a)$ を用いる
$f(x)=\sqrt{x}$ とおくと、$f(1)=\sqrt{1}=1$、$f'(x)=\dfrac{1}{2\sqrt{x}}$ より $f'(1)=\dfrac{1}{2\sqrt{1}}=\dfrac{1}{2}$
$y=f'(1)(x-1)+f(1)=\dfrac{1}{2}(x-1)+1=\dfrac{1}{2}x+\dfrac{1}{2}$
(2) $y={\mathrm{sin}}x\quad(x=\dfrac{\pi}{3})$
解答
($x=a$に対応する点における接線の公式)$y=f'(a)(x-a)+f(a)$ を用いる
$f(x)={\mathrm{sin}}x$ とおくと、$f\left(\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}$、$f'(x)={\mathrm{cos}}x$ より $f’\left(\dfrac{\pi}{3}\right)={\mathrm{cos}}\left(\dfrac{\pi}{3}\right)=\dfrac{1}{2}$
$y=f’\left(\dfrac{\pi}{3}\right)\left(x-\dfrac{\pi}{3}\right)+f\left(\dfrac{\pi}{3}\right)=\dfrac{1}{2}\left(x-\dfrac{\pi}{3}\right)+\dfrac{\sqrt{3}}{2}=\dfrac{1}{2}x-\dfrac{\pi}{6}+\dfrac{\sqrt{3}}{2}$ (答)
関数の増減・極値
2. 次の関数の増減・極値を調べてグラフをかけ
(1) $y=x^3+3x^2+1$
解答
$y’=3x^2+6x=3x(x+2)=0 \Rightarrow x=-2,0$より増減表をかく
$\begin{matrix}
x & \cdots & -2 & \cdots & 0 &\cdots \\
y’ & + & 0 & – & 0 & + \\
y & \nearrow & \underset{極大}{5} & \searrow & \underset{極小}{1} & \nearrow \\
\end{matrix}$

(2) $y=x^4-2x^2$
解答
$y’=4x^3-4x=4x(x^2-1)=4x(x+1)(x-1)=0 \Rightarrow x=-1,0,1$ より増減表をかく
$\begin{matrix}
x & \cdots & -1 & \cdots & 0 &\cdots & 1 & \cdots\\y’ & – & 0 & + & 0 & – & 0 & +\\y & \searrow & \underset{極小}{-1} & \nearrow & \underset{極大}{0} & \searrow &\underset{極小}{-1} & \nearrow \\
\end{matrix}$

(3) $y=3x^4-4x^3$
解答
$y’=12x^3-12x^2=12x^2(x-1)=0 \Rightarrow x=0,1$より増減表をかく
$\begin{matrix}
x & \cdots & 0 & \cdots & 1 &\cdots \\y’ & – & 0 & – & 0 & + \\y & \searrow & 0 & \searrow & \underset{極小}{-1} & \nearrow \\\end{matrix}$

極限値(ロピタルの定理)
注意:$\dfrac{0}{0}, \dfrac{\infty}{\infty}$ の不定形であっても、次の場合はロピタルの定理を適用することはできない
(1) $\displaystyle{\lim_{x\to a}}\dfrac{f'(x)}{g'(x)}$ が振動する場合
(2) $a$ のいくらでも”近く”に $a$ と異なる $g'(x)=0$ の解が存在する場合
例
(1) $\displaystyle{\lim_{x\to \infty}}\dfrac{x+{\mathrm{sin}}x}{x}=1$ しかし、$\displaystyle{\lim_{x\to \infty}}\dfrac{(x+{\mathrm{sin}}x)’}{(x)’}=\displaystyle{\lim_{x\to \infty}}(1+{\mathrm{cos}}x)$ は振動する
(コーシーの平均値の定理の$’c=c_x’$ は、$a$ に近づくが、$x$ に依存して決まるので、特別な近づき方をしていることが原因)
(2) $\displaystyle{\lim_{x\to \infty}}\dfrac{x+\dfrac{1}{2}{\mathrm{sin}}2x}{\left(x+\dfrac{1}{2}{\mathrm{sin}}2x\right)e^{{\mathrm{sin}}x}}=\displaystyle{\lim_{x\to \infty}}\dfrac{1}{e^{{\mathrm{sin}}x}}$ は振動するが、
$\displaystyle{\lim_{x\to \infty}}\dfrac{\left(x+\dfrac{1}{2}{\mathrm{sin}}2x \right)^{\prime}}{\left \lbrace \left(x+\dfrac{1}{2}{\mathrm{sin}}2x \right)e^{{\mathrm{sin}}x} \right\rbrace ^{\prime}}=\displaystyle{\lim_{x\to \infty}}\dfrac{2{\mathrm{cos}}^2x}{{\mathrm{cos}}x \left( 2{\mathrm{cos}}x +x+\dfrac{1}{2}{\mathrm{sin}}2x\right)e^{{\mathrm{sin}}x}}=0$
($a$ の”十分近く”で $x\ne a$ であれば、$g'(x) \ne 0$ が成り立たなければ、コーシーの平均値の定理を適用できないことが原因)
1. 次の極限値を求めよ
(1) $\displaystyle{\lim_{x\to 1}}\dfrac{x^3-1}{x-1}$
解答
$\displaystyle{\lim_{x\to 1}}\dfrac{x^3-1}{x-1}\underset{\scriptsize{\dfrac{0}{0}}}{=}\displaystyle{\lim_{x\to 1}}\dfrac{3x^2}{1}=\dfrac{3\cdot1^2}{1}=3$ (答)
(2) $\displaystyle{\lim_{x\to 0}}\dfrac{{\mathrm{sin}}3x}{{\mathrm{tan}}2x}$
解答
$\displaystyle{\lim_{x\to 0}}\dfrac{{\mathrm{sin}}3x}{{\mathrm{tan}}2x}\underset{\scriptsize{\dfrac{0}{0}}}{=}\displaystyle{\lim_{x\to 0}}\dfrac{3{\mathrm{cos}}3x}{\dfrac{2}{{\mathrm{cos}}^{2}2x}}\underset{{\mathrm{cos}}0=1}{=}\dfrac{3\cdot 1}{\dfrac{2}{1^2}}=\dfrac{3}{2}$ (答)
(3) $\displaystyle{\lim_{x\to 0}}\dfrac{1-{\mathrm{cos}}^2x}{x^2}$
解答
$\displaystyle{\lim_{x\to 0}}\dfrac{1-{\mathrm{cos}}^2x}{x^2}\underset{\scriptsize{\dfrac{0}{0}}}{=}\displaystyle{\lim_{x\to 0}}\dfrac{2{\mathrm{sin}}x{\mathrm{cos}}x}{2x}\underset{\scriptsize{\dfrac{0}{0}}}{=}\displaystyle{\lim_{x\to 0}}\dfrac{2{\mathrm{cos}}^2x-2{\mathrm{sin}}^2x}{2}=\dfrac{2\cdot 1^2-2\cdot 0^2}{2}=1$ (答)
(4) $\displaystyle{\lim_{x\to \infty}}\dfrac{e^{2x}}{x^2}$
解答
$\displaystyle{\lim_{x\to \infty}}\dfrac{e^{2x}}{x^2}\underset{\scriptsize{\dfrac{\infty}{\infty}}}{=}\displaystyle{\lim_{x\to \infty}}\dfrac{2e^{2x}}{2x}\underset{\scriptsize{\dfrac{\infty}{\infty}}}{=}\displaystyle{\lim_{x\to \infty}}\dfrac{4e^{2x}}{2}=\infty$ (答)
(5) $\displaystyle{\lim_{x\to +0}}x{\mathrm{log}}x$
「$+0\cdot\infty=\dfrac{\infty}{\dfrac{1}{+0}}=\dfrac{\infty}{\infty}$ 不定形」に注意する
解答
$\displaystyle{\lim_{x\to +0}}x{\mathrm{log}}x=\displaystyle{\lim_{x\to +0}}\dfrac{{\mathrm{log}}x}{\dfrac{1}{x}}\underset{\scriptsize{\dfrac{\infty}{\infty}}}{=}\displaystyle{\lim_{x\to +0}}\dfrac{\dfrac{1}{x}}{\dfrac{-1}{x^2}}\underset{\scriptsize{\dfrac{1}{x}}\div\scriptsize{\dfrac{-1}{x^2}}=-x}{=}\displaystyle{\lim_{x\to +0}}(-x)=0$ (答)
関数の最大・最小
2. 次の関数の指定された区間における最大値と最小値を求めよ
(1) $y=x\sqrt{1-x^2}\quad(-1\leq x \leq1)$
解答
$y’=\sqrt{1-x^2}+x\cdot\dfrac{-\cancel{2}x}{\cancel{2}\sqrt{1-x^2}}=\dfrac{1-x^2}{\sqrt{1-x^2}}+\dfrac{-x^2}{\sqrt{1-x^2}}=\dfrac{(1+\sqrt{2}x)(1-\sqrt{2}x)}{\sqrt{1-x^2}}=0$
$ \Rightarrow x=-\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}=-\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}$ より区間 $\lbrack -1, 1 \rbrack$ で増減表をかく
$\begin{matrix}
x & -1 &\cdots & -\dfrac{\sqrt{2}}{2} & \cdots & \dfrac{\sqrt{2}}{2} &\cdots & 1\\
y’ & \cancel{} & – & 0 & + & 0 & – & \cancel{} \\
y & 0 & \searrow & \underset{最小値}{-\dfrac{1}{2}} & \nearrow & \underset{最大値}{\dfrac{1}{2}} & \searrow & 0 \\
\end{matrix}$
増減表より $x=-\dfrac{\sqrt{2}}{2}$ のとき 最小値 $-\dfrac{1}{2}$、$x=\dfrac{\sqrt{2}}{2}$ のとき 最大値 $\dfrac{1}{2}$ (答)
(2) $y=\dfrac{2x}{x^2+1}\quad(-2\leq x \leq2)$
解答
$y’=\dfrac{2(x^2+1)-2x\cdot2x}{(x^2+1)^2}=\dfrac{-2x^2+2}{(x^2+1)^2}=\dfrac{-2(x+1)(x-1)}{(x^2+1)^2}=0$
$ \Rightarrow x=-1,1$ より区間 $\lbrack -2, 2 \rbrack$ で増減表をかく
$\begin{matrix}
x & -2 &\cdots & -1 & \cdots & 1 &\cdots & 2\\
y’ & \cancel{} & – & 0 & + & 0 & – & \cancel{} \\
y & -\dfrac{4}{5} & \searrow & \underset{最小値}{-1} & \nearrow & \underset{最大値}{1} & \searrow & \dfrac{4}{5} \\
\end{matrix}$
増減表より $x=-1$ のとき 最小値 $-1$、$x=1$ のとき 最大値 $1$ (答)
ベクトルの平行条件・垂直条件
1. 3点 ${\mathrm{A}}(1, 3), {\mathrm{B}}(3, y), {\mathrm{C}}(7, 5)$ について次の問いに答えよ
(1) 3点 ${\mathrm{A}}, {\mathrm{B}}, {\mathrm{C}}$ が一直線上に並ぶように $y$ の値を定めよ
解答
(公式) 3点 ${\mathrm{A}}, {\mathrm{B}}, {\mathrm{C}}$ が一直線上に並ぶ $\iff \overrightarrow{\mathrm{AB}}/\!/\overrightarrow{\mathrm{AC}} \quad \left( \overrightarrow{\mathrm{AB}}=t\overrightarrow{\mathrm{AC}} \right)$
$\quad \quad \quad \begin{pmatrix}a_1\\a_2\end{pmatrix} /\!/ \begin{pmatrix}b_1\\b_2\end{pmatrix}$ かつ $ b_1\cdot b_2 \ne 0 \iff \dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}$
$\overrightarrow{\mathrm{AB}}=\begin{pmatrix}3\\y\end{pmatrix}-\begin{pmatrix}1\\3\end{pmatrix}=\begin{pmatrix}2\\y-3\end{pmatrix}, \; \overrightarrow{\mathrm{AC}}=\begin{pmatrix}7\\5\end{pmatrix}-\begin{pmatrix}1\\3\end{pmatrix}=\begin{pmatrix}6\\2\end{pmatrix},\quad \overrightarrow{\mathrm{AB}}/\!/\overrightarrow{\mathrm{AC}}\;$ なので
$\dfrac{2}{6}=\dfrac{y-3}{2} \Rightarrow 2=3(y-3) \Rightarrow y=\dfrac{11}{3}$ (答)
(2) $\triangle{\mathrm{ABC}}$ が ${\mathrm{B}}=90^{\circ}$ である直角三角形となるように $y$ の値を定めよ
解答
(公式) $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}$、$\vec{a}\perp\vec{b} \iff \vec{a}\cdot\vec{b}=0$
$\overrightarrow{\mathrm{BA}}=\begin{pmatrix}1\\3\end{pmatrix}-\begin{pmatrix}3\\y\end{pmatrix}=\begin{pmatrix}-2\\3-y\end{pmatrix}, \overrightarrow{\mathrm{BC}}=\begin{pmatrix}7\\5\end{pmatrix}-\begin{pmatrix}3\\y\end{pmatrix}=\begin{pmatrix}4\\5-y\end{pmatrix}$ なので
$\overrightarrow{\mathrm{BA}}\cdot\overrightarrow{\mathrm{BC}}=\begin{pmatrix}-2\\3-y\end{pmatrix}\cdot\begin{pmatrix}4\\5-y\end{pmatrix}=0 \Rightarrow (-2)\cdot4+(3-y)(5-y)=0 \Rightarrow$
$y^2-8y+7=(y-1)(y-7)=0 \Rightarrow y=1,7$ (答)
ベクトルの長さ
2. 3点 ${\mathrm{A}}(1, -1), {\mathrm{B}}(3, 1), {\mathrm{C}}(-2, 2)$ を頂点とする三角形はどんな三角形か
解答
(公式) $\left |\begin{pmatrix}a_1\\a_2\end{pmatrix}\right |=\sqrt{a_1^2+a_2^2}$ 、$\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}$
$\overrightarrow{\mathrm{AB}}=\begin{pmatrix}3\\1\end{pmatrix}-\begin{pmatrix}1\\-1\end{pmatrix}=\begin{pmatrix}2\\2\end{pmatrix},\quad {\mathrm{AB}}^2=\left|\overrightarrow{\mathrm{AB}}\right|^2=2^2+2^2=8 $
$\overrightarrow{\mathrm{AC}}=\begin{pmatrix}-2\\2\end{pmatrix}-\begin{pmatrix}1\\-1\end{pmatrix}=\begin{pmatrix}-3\\3\end{pmatrix},\quad {\mathrm{AC}}^2=\left|\overrightarrow{\mathrm{AC}}\right|^2=(-3)^2+3^2=18$
$\overrightarrow{\mathrm{BC}}=\begin{pmatrix}-2\\2\end{pmatrix}-\begin{pmatrix}3\\1\end{pmatrix}=\begin{pmatrix}-5\\1\end{pmatrix},\quad {\mathrm{BC}}^2=\left|\overrightarrow{\mathrm{BC}}\right|^2=(-5)^2+1^2=26$
以上より ${\mathrm{BC}}^2={\mathrm{AB}}^2+{\mathrm{AC}}^2$ が成り立つので、${\mathrm{A}}=90^{\circ}$ の直角三角形 (答)
分点の位置ベクトル
3. 3点 ${\mathrm{A}}(1, 2), {\mathrm{B}}(5, 2), {\mathrm{C}}(3, 2)$ について次の問いに答えよ
(1) ${\mathrm{AB}}$ を 1:3 に内分する点 ${\mathrm{P}}$ の位置ベクトルを求めよ
解答
(公式) ${\mathrm{AB}}$ を $n:m$ に内分する点 ${\mathrm{P}}$ の位置ベクトル: $\overrightarrow{\mathrm{OP}}=\dfrac{m}{n+m}\overrightarrow{\mathrm{OA}}+\dfrac{m}{n+m}\overrightarrow{\mathrm{OB}}$
$\overrightarrow{\mathrm{OP}}=\dfrac{3}{1+3}\begin{pmatrix}1\\2\end{pmatrix}+\dfrac{1}{1+3}\begin{pmatrix}5\\2\end{pmatrix}=\begin{pmatrix}\dfrac{3\cdot1+1\cdot5}{4}\\\dfrac{3\cdot2+1\cdot2}{4}\end{pmatrix}=\begin{pmatrix}2\\2\end{pmatrix}$ (答)
(2) ${\mathrm{AB}}$ を 1:3 に外分する点 ${\mathrm{Q}}$ の位置ベクトルを求めよ
解答
(公式) ${\mathrm{AB}}$ を $n:m$ に外分する場合は、$n$ と $m$ の小さい方にマイナスを付けて
$\quad \quad \quad$(内)分点の公式を適用する
$\overrightarrow{\mathrm{OQ}}=\dfrac{3}{-1+3}\begin{pmatrix}1\\2\end{pmatrix}+\dfrac{-1}{-1+3}\begin{pmatrix}5\\2\end{pmatrix}=\begin{pmatrix}\dfrac{3\cdot1+(-1)\cdot5}{2}\\\dfrac{3\cdot2+(-1)\cdot2}{2}\end{pmatrix}=\begin{pmatrix}-1\\2\end{pmatrix}$ (答)
(3) $\triangle{\mathrm{ABC}}$ の重心 ${\mathrm{G}}$ の位置ベクトルを求めよ
解答
(公式) $\triangle{\mathrm{ABC}}$ の重心 ${\mathrm{G}}$ の位置ベクトル: $\overrightarrow{\mathrm{OG}}=\dfrac{1}{3}\left(\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}\right)$
$\overrightarrow{\mathrm{OG}}=\dfrac{1}{3}\left \lbrace \begin{pmatrix}1\\2\end{pmatrix}+\begin{pmatrix}5\\2\end{pmatrix}+\begin{pmatrix}3\\2\end{pmatrix}\right \rbrace=\begin{pmatrix}\dfrac{1+5+3}{3}\\\dfrac{2+2+2}{3}\end{pmatrix}=\begin{pmatrix}3\\2\end{pmatrix}$ (答)
直線の方向ベクトと法線ベクトル
4. 3点 ${\mathrm{A}}(1, 3), {\mathrm{B}}(4, 5), {\mathrm{C}}(2, -1)$ について次の問いに答えよ
(1) $\overrightarrow{\mathrm{AB}}$ を方向ベクトルとし、点 ${\mathrm{C}}$ を通る直線の方程式を求めよ
解答
(公式) 点 ${\mathrm{P}}_0(x_0, y_0)$ を通り、方向ベクトル $\vec{v}=\begin{pmatrix}a\\b\end{pmatrix}$ の直線: $\dfrac{x-x_0}{a}=\dfrac{y-y_0}{b}$
$\vec{v}=\overrightarrow{\mathrm{AB}}=\begin{pmatrix}4\\5\end{pmatrix}-\begin{pmatrix}1\\3\end{pmatrix}=\begin{pmatrix}3\\2\end{pmatrix}$ より
$\dfrac{x-2}{3}=\dfrac{y+1}{2} \Rightarrow 2(x-2)=3(y+1) \Rightarrow 2x-3y-7=0 \Rightarrow y=\dfrac{2}{3}x-\dfrac{7}{3}$ (答)
(2) $\overrightarrow{\mathrm{AB}}$ を法線ベクトルとし、点 ${\mathrm{C}}$ を通る直線の方程式を求めよ
解答
(公式) 点 ${\mathrm{P}}_0(x_0, y_0)$ を通り、法線ベクトル $\vec{n}=\begin{pmatrix}a\\b\end{pmatrix}$ の直線: $a(x-x_0)+b(y-y_0)=0$
$\vec{n}=\overrightarrow{\mathrm{AB}}=\begin{pmatrix}4\\5\end{pmatrix}-\begin{pmatrix}1\\3\end{pmatrix}=\begin{pmatrix}3\\2\end{pmatrix}$ より
$3(x-2)+2(y+1)=0 \Rightarrow 3x+2y-4=0 \Rightarrow y=\dfrac{-3}{2}x+2$ (答)
2点を直径の両端とする円
5. 2点 ${\mathrm{A}}(-5, 2), {\mathrm{B}}(3, -6)$ を直径の両端とする円の方程式を求めよ
解答
(公式) ${\mathrm{A}}(a_1, a_2) {\mathrm{B}}(b_1, b_2)$ を直径の両端とする円: $(x-a_1)(x-b_1)+(y-a_2)(y-b_2)=0$
$(x+5)(x-3)+(y-2)(y+6)=0 \Rightarrow x^2+y^2+2x+4y-27=0$ (答)
$\left( \Rightarrow (x+1)^2+(y+2)^2=32 \Rightarrow 中心\:(-1,-2) \; 半径\:\sqrt{32}=4\sqrt{2} \; の円\right)$





