等差数列
1.初項$2$、公差$-3$の等差数列について次の問いに答えよ。
(1) 一般項$a_n$を求めよ。
解答
公式 $a_n=dn+(a-d)$ において、$a=2, d=-3$ を代入して
$a_n=-3n+5$ (答)
(2) $-40$ はこの数列の第何項か。
解答
(1)より$a_n=-3n+5$だから、方程式$-40=-3n+5$を解いて、
$3n=40+5$ より $n=15$ だから、第15項(答)
(3)第1項から第$n$項までの和$S_n$を求めよ。
解答
$S_n=\dfrac{1}{2}n(a+a_n)$だから、(1)より$a_n=-3n+5$、
また $a=2$ なので $S_n=\dfrac{1}{2}n(-3n+7)$(答)
(4) 第6項から第25項までの和$S$を求めよ。
解答
和の最初の項を$s$、最後の項を$t$、項数を$n$とすると、$S=\dfrac{1}{2}n(s+t)$
$s=a_{6}=-3\cdot6+5=-13$、$t=a_{25}=-3\cdot25+5=-70$、
$n=25-6+1=20$ より $S=\dfrac{1}{2}\cdot20(-13-70)=-830$(答)
2.第3項が5、第11項が29の等差数列の初項 $a$ と公差 $d$ を求めよ。
解答
連立方程式 $\left\{ \begin{array}{l} a_3=a+2d=5 \\ a_{11}=a+10d=29 \end{array} \right.$ を解いて、$a=-1$、$d=3$(答)
等比数列
1.初項$3$、公比$2$の等比数列について次の問いに答えよ。
(1)一般項 $a_n$ を求めよ。
解答
公式 $a_n=a\cdot r^{n-1}$ において、$a=3, r=2$ を代入して
$a_n=3\cdot2^{n-1}$(答)
(2)$192$ はこの数列の第何項か。
解答
$a_n=3\cdot2^{n-1}=192$ より $2^{n-1}=\dfrac{192}{3}=64=2^6$
よって $n-1=6$ だから $n=7$ 第7項(答)
(3)第1項から第$n$項までの和$S_n$を求めよ。
解答
$S_n=a\cdot\dfrac{r^n-1}{r-1}=3\cdot\dfrac{2^n-1}{2-1}=3(2^n-1)$
2.第3項が5、第8項が160の等差比列の初項 $a$ と公比 $r$ (実数) を求めよ。
解答
連立方程式$\left\{ \begin{array}{l} a_3=ar^2=5&\cdots\textstyle{①} \\ a_{8}=ar^7=160&\cdots\textstyle{②} \end{array} \right.$ を解く $\dfrac{\textstyle{②}}{\textstyle{①}}$ より
$r^5=\dfrac{ar^7}{ar^2}=\dfrac{160}{5}=32=2^5$ よって $r=2$(答)
さらに ${\textstyle{①}}$ に代入して $a=\dfrac{5}{4}$(答)
和 $\Sigma$ の記号
1.次の和を求めよ。
(1) $\displaystyle{\sum_{k=1}^{n}(4k-1)}$
解答
(公式) $\displaystyle{\sum_{k=1}^{n}k}=\dfrac{1}{2}n(n+1)$ および $\displaystyle{\sum_{k=1}^{n}c}=cn$ を用いる
$\displaystyle{\sum_{k=1}^{n}(4k-1)}=4\displaystyle{\sum_{k=1}^{n}k}-\displaystyle{\sum_{k=1}^{n}1}=4\cdot\dfrac{1}{2}n(n+1)-1\cdot n$
$=2n(n+1)-n=n(2n+2-1)=n(2n+1)$(答)
(2) $\displaystyle{\sum_{k=1}^{n}k(3k+1)}$
解答
(公式) $\displaystyle{\sum_{k=1}^{n}k}=\dfrac{1}{2}n(n+1)$ および $\displaystyle{\sum_{k=1}^{n}k^2}=\dfrac{1}{6}n(n+1)(2n+1)$ を用いる
$\displaystyle{\sum_{k=1}^{n}k(3k+1)}=3\displaystyle{\sum_{k=1}^{n}k^2}+\displaystyle{\sum_{k=1}^{n}k}=3\cdot\dfrac{1}{6}n(n+1)(2n+1)+\dfrac{1}{2}n(n+1)$
$=\dfrac{1}{2}n(n+1)(2n+1+1)=\dfrac{1}{2}n(n+1)2(n+1)=n(n+1)^2$(答)
(3) $\displaystyle{\sum_{k=1}^{n}\dfrac{1}{(3k+1)(3k+4)}}$
解答
(公式) $a_{k+1}-a_k=d$ のとき $\displaystyle{\sum_{k=1}^{n}}\dfrac{1}{a_ka_{k+1}}=\dfrac{1}{d}\left(\dfrac{1}{a_1}-\dfrac{1}{a_{n+1}}\right)$ を用いる
$a_k=3k+1$ とおくと $a_{k+1}=3(k+1)+1=3k+4$ より
$\displaystyle{\sum_{k=1}^{n}\dfrac{1}{(3k+1)(3k+4)}}=\displaystyle{\sum_{k=1}^{n}}\dfrac{1}{a_ka_{k+1}}=\dfrac{1}{d}\left(\dfrac{1}{a_1}-\dfrac{1}{a_{n+1}}\right)$ だから
この式に、$d=a_{k+1}-a_k=3k+4-(3k+1)=3$、$a_1=3\cdot1+1=4$
および $a_{n+1}=3n+4$ を代入して、
$\displaystyle{\sum_{k=1}^{n}\dfrac{1}{(3k+1)(3k+4)}}=\dfrac{1}{3}\left(\dfrac{1}{4}-\dfrac{1}{3n+4}\right)=\dfrac{1}{3}\cdot\dfrac{3n+4-4}{4(3n+4)}=\dfrac{n}{4(3n+4)}$(答)
(4) $\displaystyle{\sum_{k=1}^{n}\dfrac{1}{\sqrt{3k+4}+\sqrt{3k+1}}}$
解答
$\dfrac{1}{\sqrt{3k+4}+\sqrt{3k+1}}=\dfrac{1}{\sqrt{3k+4}+\sqrt{3k+1}}\cdot\dfrac{\sqrt{3k+4}-\sqrt{3k+1}}{\sqrt{3k+4}-\sqrt{3k+1}}$
$=\dfrac{\sqrt{3k+4}-\sqrt{3k+1}}{(3k+4)-(3k+1)}=\dfrac{\sqrt{3k+4}-\sqrt{3k+1}}{3}=\dfrac{-1}{3}\left(\sqrt{3k+1}-\sqrt{3k+4}\right)$
$=\dfrac{-1}{3}\left(a_k-a_{k+1}\right)$ ($a_k=\sqrt{3k+1} $、$a_{k+1}=\sqrt{3(k+1)+1}=\sqrt{3k+4}$ )よって
$\displaystyle{\sum_{k=1}^{n}}\dfrac{1}{\sqrt{3k+4}+\sqrt{3k+1}}=\displaystyle{\sum_{k=1}^{n}}\dfrac{-1}{3}(a_k-a_{k+1})$
$=\dfrac{-1}{3}\{(a_1-a_2)+(a_2-a_3)+\cdots+(a_n-a_{n+1})\}=\dfrac{-1}{3}(a_1-a_{n+1})$
$=\dfrac{a_{n+1}-a_1}{3}=\dfrac{\sqrt{3n+4}-\sqrt{4}}{3}=\dfrac{\sqrt{3n+4}-2}{3}$(答)
漸化式と数学的帰納法
1.次の漸化式を解け。
(1) $a_1=1,\;a_{n+1}=a_n+2n-1$
解答
(公式) $b_k=a_{k+1}-a_k$ のとき $a_n=a_1+\displaystyle{\sum_{k=1}^{n-1}}b_k$ を用いる
$a_{n+1}=a_n+2n-1$ より $a_{n+1}-a_n=2n-1$ これに $n=k$ を代入して
$b_k=a_{k+1}-a_k=2k-1$ となるので、
$a_n=a_1+\displaystyle{\sum_{k=1}^{n-1}}b_k=1+\displaystyle{\sum_{k=1}^{n-1}}(2k-1)=1+2\displaystyle{\sum_{k=1}^{n-1}}k-\displaystyle{\sum_{k=1}^{n-1}}1$
$=1+2\cdot\dfrac{1}{2}(n-1)n-1\cdot(n-1)=1+(n-1)n-n+1=n^2-2n+2$(答)
(2) $a_1=2,\;a_{n+1}=2a_n-1$
解答
(公式) $a_{n+1}=ra_n+b\;(r \neq 1)$ のとき $a_n-\lambda=(a_1-\lambda)r^{n-1}$ を用いる
ただし、$\lambda=r\lambda+b$
$a_{n+1}=2a_n-1$ より $\lambda=2\lambda-1$ を解くと $\lambda=1$ よって、
$a_n-1=(a_1-1)2^{n-1}=(2-1)2^{n-1}=2^{n-1}$ だから $a_n=2^{n-1}+1$(答)
2.次の問いに答えよ。
(1) 漸化式 $a_1=1,\; a_{n+1}=\dfrac{a_n}{3a_n+1}$ の解は
$a_n=\dfrac{1}{3n-2}$ であることを数学的帰納法で証明せよ
解答
$a_n=\dfrac{1}{3n-2}\cdots(*)$ とおく
(1) $n=1$ のとき $((*)$の左辺$)=a_1=1$ $((*)$の右辺$)=\dfrac{1}{3\cdot1-2}=\dfrac{1}{1}=1$
$\quad$よって (左辺)$=$(右辺) だから $n=1$ のとき $(*)$ が成り立つ
(2) $n=k$ のとき、$a_k=\dfrac{1}{3k-2}\cdots$① が成り立つと仮定する 漸化式と①より
$\quad a_{k+1}=\dfrac{a_k}{3a_k+1}=\dfrac{\dfrac{1}{3k-2}}{3\cdot\dfrac{1}{3k-2}+1}\cdot\dfrac{3k-2}{3k-2}=\dfrac{1}{3+3k-2}=\dfrac{1}{3k+1}=\dfrac{1}{3(k+1)-2}$
$\quad$よって、$a_{k+1}=((*)$で $n=k+1$ とおいた式の右辺$)$ が成り立つので、
$\quad$$(*)$ は $n=k+1$ のときも成り立つ
(3) (1)(2) よりすべての自然数 $n$ について $(*)$ が成り立つ (証明終)
(2) $1+2+\cdots+n=\dfrac{1}{2}n(n+1)$ を数学的帰納法で証明せよ
解答
$1+2+\cdots+n=\dfrac{1}{2}n(n+1)=\dfrac{1}{2}n(n+1)\cdots(*)$ とおく
(1) $n=1$ のとき $((*)$の左辺$)=1$ $((*)$の右辺$)=\dfrac{1}{2}\cdot1\cdot(1+1)=1$
$\quad$よって (左辺)$=$(右辺) だから $n=1$ のとき $(*)$ が成り立つ
(2) $n=k$ のとき、$1+2+\cdots+k=\dfrac{1}{2}k(k+1)\cdots$① が成り立つと仮定する
$\quad$①の両辺に $(k+1)$ をたすと
$1+2+\cdots+k+(k+1)=\dfrac{1}{2}k(k+1)+(k+1)=\left(\dfrac{1}{2}k+1\right)(k+1)=\dfrac{1}{2}(k+2)(k+1)$
$\quad$よって、$1+2+\cdots+k+(k+1)=((*)$で $n=k+1$ とおいた式の右辺$)$ が成り立つので、
$\quad$$(*)$ は $n=k+1$ のときも成り立つ
(3) (1)(2) よりすべての自然数 $n$ について $(*)$ が成り立つ (証明終)
データの整理
1.数値データ $\{1,1,1,2,3,4,4,4,5,5\}$ 次の問いに答えよ。
(1) 度数分布表を作り、平均$=\mu$、分散$=\sigma^2$、標準偏差$=\sigma$ および最頻値$=m$ を求めよ
解答
データラベルが $x$ のとき (公式) 分散$=\sigma^2=\mu_{x^2}-(\mu_x)^2$ を用いる
データラベルを $x$、度数を $f$ として度数分布表を作る 表より 最頻値$=m=1,4$(答)
| $x$ |
1 |
2 |
3 |
4 |
5 |
計 |
| $f$ |
3 |
1 |
1 |
3 |
2 |
10 |
| $xf$ |
3 |
2 |
3 |
12 |
10 |
30 |
| $x^2f$ |
3 |
4 |
9 |
48 |
50 |
114 |
$x$の平均$=\mu=\mu_x=\dfrac{xfの合計}{fの合計}=\dfrac{30}{10}=3$(答)、$x^2$の平均$=\mu_{x^2}=\dfrac{x^2fの合計}{fの合計}=\dfrac{114}{10}=11.4$
よって、分散$=\sigma^2=\mu_{x^2}-(\mu_x)^2=11.4-3^2=2.4$(答)、標準偏差$=\sigma=\sqrt{\sigma^2}=\sqrt{2.4}$(答)
注意:分散の定義は「(偏差の2乗)$=(x-\mu)^2$」の平均なので、下のように定義から直接求めても良い
$\quad \quad \sigma^2=\dfrac{(x-\mu)^2fの合計}{fの合計}=\dfrac{24}{10}=2.4$
(2) 最大値=Max・最小値=Minおよび中央値$=Q_2$、第1四分位数$=Q_1$、第3四分位数$=Q_3$ を求めよ
解答
最大値=Max$=5$、最小値=Min$=1$ (答) データの個数は10個と偶数なので、
中央値は5番目と6番目の平均をとって、$Q_2=\dfrac{3+4}{2}=3.5$(答)
第1四分位数は前半5個の中央値なので、3番目の値だから $Q_1=1$(答)
第4四分位数は後半5個の中央値なので、8番目の値だから $Q_3=4$(答)
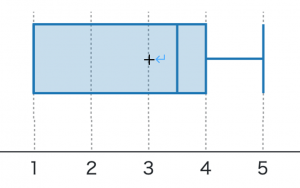
(3)箱ヒゲ図を書け
解答
Min$=Q_1=1$、$\mu=3$、$Q_2=3.5$、$Q_3=4$、Max$=5$ に注意する
2. $y=\dfrac{x-30}{5}$ と変数変換して $y$ に関する平均 $E(y)$ と分散 $V(y)$ を求めたら
$\; E(y)=3, V(y)=2$ であった。 $x$ に関する平均 $E(x)$ と分散 $V(x)$ を求めよ。
解答
(公式) $E(ax+b)=aE(x)+b$ および $V(ax+b)=a^2V(x)$ を用いる
$y=\dfrac{x-30}{5}$ より $x=5y+30$ だから、公式を適用すると
$E(x)=E(5y+30)=5E(y)+30=5\cdot3+30=45$ (答)
$V(x)=V(5y+30)=5^2\cdot V(y)=25\cdot2=50$ (答)
数列の極限と関数の極限
1.次の極限を求めよ。
(1) $\displaystyle{\lim_{n \to \infty}}\dfrac{3n^2-5n+2}{2n^2+n+1}$
解答
$\displaystyle{\lim_{n \to \infty}}\dfrac{3n^2-5n+2}{2n^2+n+1}=\displaystyle{\lim_{n \to \infty}}\dfrac{(3n^2-5n+2)\times \dfrac{1}{n^2}}{(2n^2+n+1)\times \dfrac{1}{n^2}}=\displaystyle{\lim_{n \to \infty}}\dfrac{3-\dfrac{5}{n}+\dfrac{2}{n^2}}{2+\dfrac{1}{n}+\dfrac{1}{n^2}}$
$=\dfrac{3-0+0}{2+0+0}=\dfrac{3}{2}$ (答)
(2) $\displaystyle{\lim_{n \to \infty}}\dfrac{7^{n+3}-5^n}{7^{n+2}+5^{n+1}}$
解答
$\displaystyle{\lim_{n \to \infty}}\dfrac{7^{n+3}-5^n}{7^{n+2}+5^{n+1}}=\displaystyle{\lim_{n \to \infty}}\dfrac{(7^{n+3}-5^n)\times\dfrac{1}{7^n}}{(7^{n+2}+5^{n+1})\times\dfrac{1}{7^n}}=\displaystyle{\lim_{n \to \infty}}\dfrac{7^3-\left(\dfrac{5}{7}\right)^n}{7^2+5\cdot\left(\dfrac{5}{7}\right)^n}$
$=\dfrac{7^3-0}{7^2+5\cdot0}=7$ (答)
(3) $\displaystyle{\lim_{x \to 4}}\dfrac{x^2-x-12}{x-4}$
解答
$\displaystyle{\lim_{x \to 4}}\dfrac{x^2-x-12}{x-4}=\displaystyle{\lim_{x \to 4}}\dfrac{\bcancel{(x-4)}(x+3)}{\bcancel{x-4}}=\displaystyle{\lim_{x \to 4}}(x+3)=4+3=7$ (答)
(4) $\displaystyle{\lim_{x \to \infty}}\left( \sqrt{x^2+4x+3}-\sqrt{x^2+x+1} \right)$
解答
分子を有理化する
$\displaystyle{\lim_{x \to \infty}}\dfrac{\sqrt{x^2+4x+3}-\sqrt{x^2+x+1}}{1}$
$=\displaystyle{\lim_{x \to \infty}}\dfrac{\sqrt{x^2+4x+3}-\sqrt{x^2+x+1}}{1}\times\dfrac{\sqrt{x^2+4x+3}+\sqrt{x^2+x+1}}{\sqrt{x^2+4x+3}+\sqrt{x^2+x+1}}$
$=\displaystyle{\lim_{x \to \infty}}\dfrac{(x^2+4x+3)-(x^2+x+1)}{\sqrt{x^2+4x+3}+\sqrt{x^2+x+1}}=\displaystyle{\lim_{x \to \infty}}\dfrac{3x+2}{\sqrt{x^2+4x+3}+\sqrt{x^2+x+1}}$
$=\displaystyle{\lim_{x \to \infty}}\dfrac{(3x+2)\times\dfrac{1}{x}}{\left(\sqrt{x^2+4x+3}+\sqrt{x^2+x+1}\right)\times\dfrac{1}{x}}$
$=\displaystyle{\lim_{x \to \infty}}\dfrac{3+\dfrac{2}{x}}{\sqrt{1+\dfrac{4}{x}+\dfrac{3}{x^2}}+\sqrt{1+\dfrac{1}{x}+\dfrac{1}{x^2}}}=\dfrac{3+0}{\sqrt{1+0+0}+\sqrt{1+0+0}}=\dfrac{3}{2}$ (答)
等比級数と無限和
1.次の等比級数の収束・発散を調べ、収束する場合はその値も求めよ。
(1) $S=2+\dfrac{3}{2}+\dfrac{9}{8}+\cdots$
解答
$-1<r<1$ならば、$S=a+ar+ar^2+\cdots=\dfrac{a}{1-r}$ を用いる
$-1<r=\dfrac{3}{4}<1$、$a=2$ だから、
$S=2+\dfrac{3}{2}+\dfrac{9}{8}+\cdots=\dfrac{2}{1-\dfrac{3}{4}}\times\dfrac{4}{4}=\dfrac{8}{4-3}=8$ (答)
(2) $S=2+\dfrac{5}{2}+\dfrac{25}{8}+\cdots$
解答
$-1<r<1$以外の場合は、$S=a+ar+ar^2+\cdots$ は「発散」することを用いる
$r=\dfrac{5}{4}\geq1$ だから、$S=2+\dfrac{5}{2}+\dfrac{25}{8}+\cdots$ は「発散」する (答)
2.次の和を求めよ。
(1) $\displaystyle{\sum_{k=1}^{n}}\left(\dfrac{1}{3k+1}-\dfrac{1}{3k+4}\right)$
解答
$a_k=3k+1$ とおくと、$a_{k+1}=3(k+1)+1=3k+4$ だから、
$\dfrac{1}{3k+1}-\dfrac{1}{3k+4}=\dfrac{1}{a_k}-\dfrac{1}{a_{k+1}}$ および
$\dfrac{1}{a_1}=\dfrac{1}{3\cdot1+1}=\dfrac{1}{4}$、$\dfrac{1}{a_{n+1}}=\dfrac{1}{3n+4}$ に注意すると
$\displaystyle{\sum_{k=1}^{n}}\left(\dfrac{1}{3k+1}-\dfrac{1}{3k+4}\right)=\displaystyle{\sum_{k=1}^{n}}\left(\dfrac{1}{a_k}-\dfrac{1}{a_{k+1}}\right)$
$=\left(\dfrac{1}{a_1}-\bcancel{\dfrac{1}{a_{2}}}\right)+\left(\bcancel{\dfrac{1}{a_2}}-\bcancel{\dfrac{1}{a_{3}}}\right)+\left(\bcancel{\dfrac{1}{a_3}}-\bcancel{\dfrac{1}{a_{4}}}\right)+\cdots+\left(\bcancel{\dfrac{1}{a_n}}-\dfrac{1}{a_{n+1}}\right)$
$=\left(\dfrac{1}{a_1}-\dfrac{1}{a_{n+1}}\right)=\dfrac{1}{4}-\dfrac{1}{3n+4}\left(=\dfrac{3n}{4(3n+4)}\right)$ (答)
(2) $\displaystyle{\sum_{k=1}^{\infty}}\left(\dfrac{1}{3k+1}-\dfrac{1}{3k+4}\right)$
解答
(1)の結果を用いる
$\displaystyle{\sum_{k=1}^{\infty}}\left(\dfrac{1}{3k+1}-\dfrac{1}{3k+4}\right)=\displaystyle{\lim_{n \to \infty}}\displaystyle{\sum_{k=1}^{n}}\left(\dfrac{1}{3k+1}-\dfrac{1}{3k+4}\right)$
$=\displaystyle{\lim_{n \to \infty}}\left(\dfrac{1}{4}-\dfrac{1}{3n+4}\right)=\dfrac{1}{4}-0=\dfrac{1}{4}$ (答)
平均変化率と微分の定義
1.関数 $y=f(x)=x^2-3x$ について、次の問いに答えよ。
(1)区間$[1,3]$における平均変化率 $\dfrac{\Delta y}{\Delta x}$ を求めよ
解答
$f(1)=1^2-3\cdot1=-2$、$f(3)=3^2-3\cdot3=0$ より
$\dfrac{\Delta y}{\Delta x}=\dfrac{f(3)-f(1)}{3-1}=\dfrac{0-(-2)}{2}=1$ (答)
(2)定義に従って、導関数 $y’=\dfrac{dy}{dx}$ を求めよ
解答
$f(x+h)=(x+h)^2-3(x-h)=(x^2-3x)+h(2x-3+h)$ より
$f(x+x)-(x^2-3x)=f(x+h)-f(x)=h(2x-3+h)$ だから
$y’=\dfrac{dy}{dx}=\displaystyle{\lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h}}=\displaystyle{\lim_{h \to 0}\dfrac{\cancel{h}(2x-3+h)}{\cancel{h}}}=2x-3$ (答)
べき関数と有理関数の微分
1.次の関数を微分せよ。
(1) $y=3x^4+2x^3-7x+1$
解答
公式 $\left( x^n \right)^{\prime}=nx^{n-1}$、$(x)’=1$、$(c)’=0$
および微分の線形性 $(af+bg)’=af’+bg’$ を用いる
$\dfrac{dy}{dx}=y’=3(x^4)’+2(x^3)’-7(x)’+(1)’=12x^3+6x^2-7$ (答)
(2) $y=\dfrac{1}{x^2}-2\sqrt[4]{x^3}$
解答
公式 $\left( x^a \right)^{\prime}=ax^{a-1}$、$\dfrac{1}{x^n}=x^{-n}$、$\sqrt[n]{x^m}=x^{\frac{m}{n}}$ を用いる
$y=x^{-2}-2x^{\frac{3}{4}}$ より
$\dfrac{dy}{dx}=y’=-2x^{-3}-\dfrac{3}{2}x^{-\frac{1}{4}}=\dfrac{-2}{x^3}-\dfrac{3}{2\sqrt[4]{x}}$ (答)
(3) $y=(x^2-x+1)^3$
解答
公式 $\left( f^n \right)^{\prime}=nf’f^{n-1}$ を用いる
$y=(x^2-x+1)^3=f^3$ とおくと、$f’=2x-1$ より $\dfrac{dy}{dx}=y’=3f’f^2=3(2x-1)(x^2-x+1)^2$ (答)
(4) $y=\dfrac{3x+2}{x^2-x+1}$
解答
公式 $\left( \dfrac{f}{g^n} \right)^{\prime}=\dfrac{f’g-nfg’}{g^{n+1}}$、$\left( \dfrac{f}{g} \right)^{\prime}=\dfrac{f’g-fg’}{g^{2}}$ を用いる
$y=\dfrac{3x+2}{x^2-x+1}=\dfrac{f}{g}$ とおくと $f’=3$、$g’=2x-1$ より
$\begin{array}{l} f’g &=& 3(x^2-x+1) &=& 3x^2-3x+3\\ fg’ &=& (3x+2)(2x-1) &=& 6x^2+x-2 \\ f’g-fg’ &=& &=&-3x^2-4x+5 \end{array}$
$\dfrac{dy}{dx}=y’=\dfrac{-3x^2-4x+5}{(x^2-x+1)^2}$ (答)
回帰分析
1.下の表は、ある試験の勉強時間 $x$ と得点 $y$ を表にしたものである。次の問いに答えよ。
| 時間 $x$ |
1 |
2 |
3 |
4 |
5 |
| 得点 $y$ |
50 |
65 |
70 |
85 |
80 |
(1) 勉強時間 $x$ の平均 $\mu_x$ と得点 $y$ の平均 $\mu_y$ を求めよ
解答
$\mu_x=\dfrac{1+2+3+4+5}{5}=\dfrac{15}{5}=3$、$\mu_y=\dfrac{50+65+70+85+80}{5}=\dfrac{350}{5}=70$ (答)
(2) 勉強時間 $x$ の分散 $\sigma_x^2$、得点 $y$ の分散 $\sigma_y^2$、$x$と$y$の共分散$\sigma_{xy}$ および 相関係数 $r$ を求めよ
解答
$\sigma_x^2=\overline{(x-\mu_x)^2}=\overline{(x-3)^2}$
$\quad=\dfrac{(1-3)^2+(2-3)^2+(3-3)^2+(4-3)^2+(5-3)^2}{5}$
$\quad=\dfrac{4+1+0+1+4}{5}=\dfrac{10}{5}=2$ (答)
$\sigma_y^2=\overline{(y-\mu_y)^2}=\overline{(y-70)^2}$
$\quad=\dfrac{(50-70)^2+(65-70)^2+(70-70)^2+(85-70)^2+(80-70)^2}{5}$
$\quad=\dfrac{400+25+0+225+100}{5}=\dfrac{750}{5}=150$ (答)
$\sigma_{xy}=\overline{(x-\mu_x)(y-\mu_y)}=\overline{(x-3)(y-70)}$
$\quad=\dfrac{(-2)\cdot(-20)+(-1)\cdot(-5)+0\cdot0+1\cdot15+2\cdot10}{5}=\dfrac{80}{5}=16$ (答)
$r=\dfrac{\sigma_{xy}}{\sqrt{\sigma_x^2}\sqrt{\sigma_y^2}}=\dfrac{16}{\sqrt{2}\sqrt{150}}=\dfrac{16}{\sqrt{300}}=\dfrac{16}{10\sqrt{3}}=\dfrac{8\sqrt{3}}{15}\left(\fallingdotseq0.92\right)$ (答)
(3) 回帰直線の方程式を求めよ
解答
公式 $y=\dfrac{\sigma_{xy}}{\sigma_x^2}(x-\mu_x)+\mu_y$ に(1)、(2)の結果を代入して
$y=\dfrac{16}{2}(x-3)+70$ より $y=8x+46$ (答)
(自由度1の)独立性のカイ2乗検定
1.飲料水AとBに関して、どちらが好きかアンケートを取った結果が下の表である。次の問いに答えよ。
|
飲料水A |
飲料水B |
計 |
| 男 |
$a=$60 |
$b=$40 |
$C=$100 |
| 女 |
$c=$40 |
$d=$10 |
$D=$50 |
| 計 |
$A=$100 |
$B=$50 |
$N=$150 |
(1) 検定統計量 $T$ の値を求めよ。
解答
検定統計量を求める簡易公式に代入して
$T=\dfrac{(ad-bc)^2N}{ABCD}=\dfrac{(60\cdot10-40\cdot40)^2\cdot150}{100\cdot50\cdot100\cdot50}=6$ (答)
(2) 帰無仮説 $H_0$: AとBの好みに関して男女差がない
$\; $対立仮説 $H_1$: AとBの好みに関して男女差がある
と設定して有意水準5%でカイ2乗検定を実施するとき、
帰無仮説 $H_0$ が棄却されるか受容されるかを判定せよ
(ただし、自由度1のカイ2乗分布の臨界値は、有意水準5%で約3.84であることを使って良い)
解答
$T=6\geq3.84$ なので、帰無仮説 $H_0$ は棄却される (答)
